Летом килограмм клубники стоит 90 рублей. Маша купила 1 кг 400 г клубники. Сколько рублей сдачи она должна была получить с 1000 рублей?

Смотреть решение

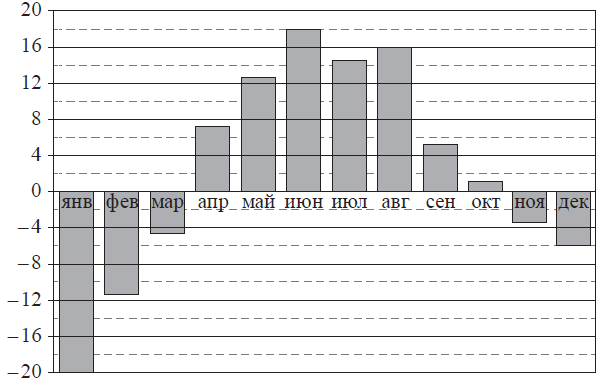
На диаграмме показана среднемесячная температура воздуха в Екатеринбурге (Свердловске) за каждый месяц 1973 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по диаграмме наименьшую среднемесячную температуру в период с мая по декабрь 1973 года включительно. Ответ дайте в градусах Цельсия.

Смотреть решение

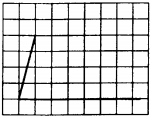
На клетчатой бумаге с размером клетки $1 \times 1$ изображён угол (см. рис.). Найдите тангенс этого угла.

Смотреть решение

В Волшебной стране бывает два типа погоды: хорошая и отличная, причём погода, установившись утром, держится неизменной весь день. Известно, что с вероятностью 0,8 погода завтра будет такой же, как и сегодня. Сегодня 3 июля, погода в Волшебной стране хорошая. Найдите вероятность того, что 6 июля в Волшебной стране будет отличная погода

Смотреть решение

Найдите корень уравнения $\sqrt{3x+88}=-x$. Если уравнение имеет более одного корня, в ответе запишите больший из корней.

Смотреть решение

Найдите площадь прямоугольной трапеции, основания которой равны 9 и 21, большая боковая сторона составляет с основанием угол 45°.

Смотреть решение

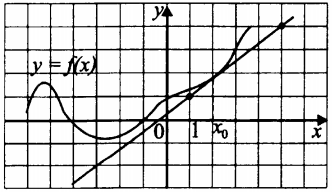
На рисунке изображены график функции $y = f(x)$ и касательная к нему в точке с абсциссой $x_{0}$. Найдите значение производной функции $f(x)$ в точке $x_{0}$.

Смотреть решение

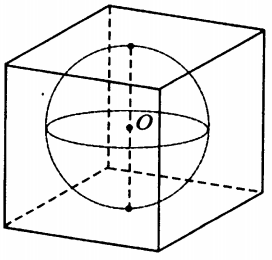
Шар, объём которого равен $36\pi$, вписан в куб (см. рис.). Найдите объём куба.

Смотреть решение

Найдите $sina$, если $cosa=\frac{2\sqrt{6}}{5}$ и $a\in(0;\frac{\pi}{2})$

Смотреть решение

Для определения эффективной температуры звёзд используют закон Стефана–Больцмана, согласно которому $P = \sigma ST^4$ , где $P$ — мощность излучения звезды (в Ваттах), $\sigma = 5,7 \cdot 10^{-8} \frac{\textrm{Вт}}{\textrm{м}^2\cdot\textrm{К}^4}$ — постоянная, $S$ — площадь поверхности звезды (в квадратных метрах), а $T$ — температура (в Кельвинах). Известно, что площадь поверхности некоторой звезды равна $\frac{1}{{16}} \cdot 10^{20}$ м$^2$, а мощность её излучения равна не менее $9,12\cdot 10^{25}$ Вт. Найдите температуру этой звезды в Кельвинах.

Смотреть решение

Первые 140 км автомобиль ехал со скоростью 50 км/ч, следующие 160 км — со скоростью 60 км/ч, а затем 120 км — со скоростью 100 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.

Смотреть решение

Найдите точку минимума функции $y=x\sqrt{x} – 9x + 724$.

Смотреть решение

а) Решите уравнение $3 \cdot 9^{x-\frac{1}{2}}-7 \cdot 6^{x}+3 \cdot 4^{x+1}=0$

б) Найдите все корни этого уравнения, принадлежащие отрезку $[2;3]$

Смотреть решение

Отрезок, соединяющий вершину $A$ ромба $ABCD$ с серединой стороны $BC$, равен стороне ромба.

а) Докажите, что высота ромба, проведенная из вершины $C$, делит сторону $AD$ на отрезки, один из которых втрое больше другого.

б) Найдите диагональ $AC$ ромба, если известно, что сторона ромба равна $\sqrt{6}$

Смотреть решение

Решите неравенство \[\frac{2^{2x+1}-96*0,5^{2x+3}+2}{x+1}\leq 0\]

Смотреть решение

Точка $M$ - центр окружности, описанной около остроугольного треугольника $NPK, Q$ - центр вписанной в него окружности, $W$ - точка пересечения высот. Известно, что $\angle PNK = \angle MPK + \angle MKP$.

а) Докажите, что точка $Q$ лежит на окружности, описанной около треугольника $PMK$

б) Найдите угол $MQW$, если $\angle NPK = 47^{o}$.

Смотреть решение

Планируется выдать льготный кредит на целое число миллионов рублей на пять лет. В середине каждого года действия кредита долг заёмщика возрастает на 20% по сравнению с началом года. В конце 1-го, 2-го и 3-го годов заёмщик выплачивает только проценты по кредиту, оставляя долг неизменно равным первоначальному. В конце 4-го и 5-го годов заёмщик выплачивает одинаковые суммы, погашая весь долг полностью. Найдите наименьший размер кредита, при котором общая сумма выплат заёмщика превысит 10 млн.

Смотреть решение

Найдите все значения параметра $a$, при каждом из которых система уравнений $\small \begin{cases} y = \sqrt{-8-6x-x^{2}}, \\ y+ax=a+1 \end{cases}$ имеет единственное решение.

Смотреть решение

Дана последовательность натуральных чисел, в которой каждое число, кроме первого и последнего, больше среднего арифметического соседних с ним членов этой последовательности.

а) Приведите пример последовательности, состоящей из пяти членов, с суммой, равной $50$.

б) Может ли в последовательности из пяти членов быть два равных между собой?

в) Какая минимальная сумма может быть в последовательности из шести членов?

Смотреть решение