Найдите все значения параметра $a$,...

Найдите все значения параметра $a$, при каждом из которых система уравнений $\small \begin{cases} y = \sqrt{-8-6x-x^{2}}, \\ y+ax=a+1 \end{cases}$ имеет единственное решение.

Построим график уравнения $y=\sqrt{-8-6x-x^{2}}$.

Преобразовав подкоренное выражение, получим: $y=\sqrt{1-(x^{2}+6x+9)}$, $y=\sqrt{1-(x+3)^{2}}$.

Если $y\geq 0$, то $y^{2} = 1 - (x+3)^{2}$, $(x+3)^{2}+y^{2}=1$.

Если $y<0$, точек, удовлетворяющих уравнению, нет.

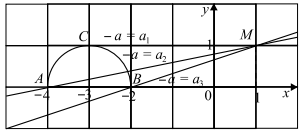
Получилась полуокружность радиусом $1$ с центром в точке $(—3; 0)$, лежащая в верхней полуплоскости (см. рис.).

Уравнение $y+ax=a+1$ запишем в виде $y=-a(x-1)+1$ — семейство прямых с угловым коэффициентом $—a$, проходящих через точку $M (1;1)$.

Рассмотрим рисунок. Видно, что система имеет единственное решение, если:

1) прямая $MC$ касается полуокружности, поэтому $-a=a_{1}=0$,

2) прямая и полуокружность имеют единственную общую точку, при этом $a_{2}< -a \leq a_{3}$.

Найдём $a_{2}$ из условия, что прямая $y=a_{2}(x-1) + 1$ проходит через точку $A(-4;0)$.

$a_{2}(-4-1)+1=0$ $a_{2}=\frac{1}{5}$.

Найдём $a_{3}$ из условия, что прямая $y = a_{3}(x-1) + 1$ проходит через точку $B(-2;0)$.

$a_{3}(-2-1)+1 = 0$ $a_{3}= \frac{1}{3}$.

Имеем $\frac{1}{5} < -a \leq \frac{1}{3}$, значит, $-\frac{1}{3} \leq a < -\frac{1}{5}$.

Следовательно, система имеет единственное решение, если $-\frac{1}{3} \leq a < -\frac{1}{5}$ и $a = 0$.

Ответ: $[-\frac{1}{3}; - \frac{1}{5})$; $0$.