ЕГЭ по Математике (профильный)
Шар, объём которого равен $36\pi$,...
Задание:
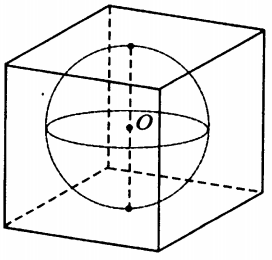
Шар, объём которого равен $36\pi$, вписан в куб (см. рис.). Найдите объём куба.
Решение:
Пусть радиус шара равен $R$, тогда объём шара находится по формуле $V_{шара}=\frac{4}{3}\pi R^{3}$.По условию $36\pi=\frac{4}{3}\pi R^{3}$. $108=4R^{3}$, $R^{3}=27$. $R=3$. Так как шар вписан в куб, то длина
ребра куба равна длине диаметра шара, но диаметр шара в два раза больше радиуса и равен $3\cdot2 = 6$. Объём куба $V$ находится по формуле $V=a^{3}$, где $a$ — ребро куба. Поэтому $V=a^{3} =6^{3} = 216$.
ребра куба равна длине диаметра шара, но диаметр шара в два раза больше радиуса и равен $3\cdot2 = 6$. Объём куба $V$ находится по формуле $V=a^{3}$, где $a$ — ребро куба. Поэтому $V=a^{3} =6^{3} = 216$.
Ответ:
216
Задание добавил(а)
Создатель и главный администратор проекта ExamMe.
О задание:
Источник условия: Книга: Математика. Подготовка к ЕГЭ-2017. Профильный уровень. 40 тренировочных вариантов. Под редакцией Ф.Ф. Лысенко, С.Ю. Калабухова.
Источник решения: Книга: Решение заданий из книги указанной в источнике условия. Автор неизвестен.
Источник решения: Книга: Решение заданий из книги указанной в источнике условия. Автор неизвестен.
Обсуждения
Только зарегистрированные пользователи могут оставлять комментарии.
