Точка $M$ - центр окружности,...

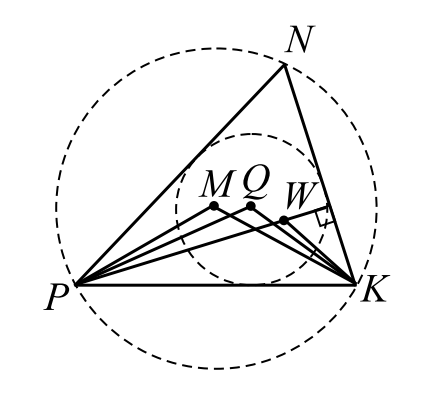
Точка $M$ - центр окружности, описанной около остроугольного треугольника $NPK, Q$ - центр вписанной в него окружности, $W$ - точка пересечения высот. Известно, что $\angle PNK = \angle MPK + \angle MKP$.

а) Докажите, что точка $Q$ лежит на окружности, описанной около треугольника $PMK$

б) Найдите угол $MQW$, если $\angle NPK = 47^{o}$.

Чтобы доказать, что точки $P, M, Q$ и $K$ лежат на одной окружности, можно воспользоваться одним из признаков, например доказать, что $\angle PMK = \angle PQK$. Найдём эти углы.

$M$ - центр окружности, описанной около треугольника $NPK$, тогда как центральный и вписанный углы, опирающиеся на одну дугу, $\angle PMK = 2 \angle PNK$.

Запишем сумму углов треугольника $PMK$ и воспользуемся полученным и заданным в условии равенствами. \[\angle PMK + \angle MPK + \angle MKP = \] \[ = 2 \angle PNK + \angle PNK = 3 \angle PNK = 180^{o} \] \[\angle PNK = 60^{o}; \angle PMK = 120^{o}\] $Q$ - центр вписанной в треугольник $NPK$ окружности, поэтому $Q$ - точка пересечения биссектрис треугольника. \[\angle PQK = 180^{o} - (\angle QPK + \angle QKP) =\] \[ = 180^{o} - \frac{\angle NPK + \angle NKP}{2}\] \[\angle PQK = 180^{o} - (\frac{180^{o} - \angle PNK}{2}) =\] \[ = 180^{o} - \frac{180^{o} - 60^{o}}{2} = 120^{o}\] Значит, $\angle PMK = \angle PQK$, поэтому точки $P, M, Q$ и $K$ лежат на одной окружности.

б) $W$ - точка пересечения высот треугольника $NPK$. Найдём угол $MQW$, для этого докажем сначала, что и точка $W$ лежит на той же окружности, что и точки $P,M,Q$ и $K$. Если провести высоту треугольника (например, из вершины $P$), то образуются прямоугольные треугольники, сумма острых углов каждого такого треугольника равна $90^{o}$. Например, $\angle WPK + \angle PKN = 90^{o}$, аналогично можно получить: $\angle WKP + \angle NPK = 90^{o}$.\[ \angle PWK = 180^{o} - \angle WPK - \angle WKP = \] \[ 180^{o} - (90^{o} - \angle PKN) - (90^{o} - \angle NPK) = \] \[ = \angle PKN + \angle NPK = 120^{o}\] $\angle PMK = \angle PQK = \angle PWK$, потому точки $P, M, Q, W$ и $K$ лежат на одной окружности.

Так как $\angle PNK = 60^{o}, \angle NPK = 47^{o}$, получаем: $\angle NKP = 73^{o}$. В равнобедренном треугольнике $PMK$ $\angle MPK = \frac{180^{o} - \angle PMK}{2} = 30^{o}$. Учитывая, что $PW \perp NK$, получаем: $\angle WPK = 90^{o} - \angle NKP = 17^{o}$.
Отсюда $\angle WPM = \angle MPK - \angle WPK = 13^{o}$
$\angle MPK = 30^{o}$, $\angle {QPK} = \frac{\angle NPK}{2} = \frac{47^{o}}{2} = 23,5^{o}$,
$\angle KPW = 90^{o} - \angle NKP = 90^{o} - 73^{o} = 17^{o}$, значит, $\angle MPK > \angle QPK > \angle KPW$, поэтому лучи $PW, PQ$ и $PM$ пересекают дугу окружности в порядке, указанном на рисунке. Четырёхугольник $PMQW$ вписан в окружность, поэтому сумма его противоположных углов равна $180^{o}$ и $\angle MQW = 180^{o} - \angle WPM = 180^{o} - 13^{o} = 167^{o}$

Ответ: $167^{o}$