Решите неравенство...

Решите неравенство $\frac{3^{x}-5^{x+1}}{4^{x}-2^{x+log_{2}5}+4} \leq 0$.

$\textit {План решения}$.

1. Отдельно преобразуем числитель и знаменатель.

1.1. В числителе вынесем за скобки $5^{x}$, чтобы в скобке осталась разность некоторого числа в степени $x$ и константы (вместо этого можно вынести за скобки $3^{x}$, а потом дополнительно преобразовать, или сразу вынести за скобки $3^{x+1}$).

1.2. В знаменателе «избавимся» от $log_{2}5$ в показателе степени (преобразуем его в множитель). После этого получим квадратичное выражение от $2^{x}$ (если сделать замену $t=2^{x}$, то получим квадратичное выражение от $t$.). Квадратичное выражение разложим на множители.

2. Все множители в числителе и знаменателе заменим более простыми, совпадающими по знаку (в том числе равными нулю одновременно с исходными — таким образом, не надо будет дополнительно думать об ОДЗ).

3. Решим неравенство, полученное на предыдущем шаге, методом интервалов.

$\textit {Решение}$

1. $\frac{3^{x}-5^{x+1}}{4^{x}-2^{x+log_{2}5}+4} \leq 0$; $\frac{((\frac{3}{5})^{x}-5)\cdot5^{x}}{2^{2x}-5\cdot 2^{x}+4} \leq 0$;
$\frac{(\frac{3}{5})^{x}-5}{(2^{x}-4)(2^{x}-1)}\leq 0$.

2. $\frac{(\frac{3}{5})^{x}-(\frac{3}{5})^{log_{\frac{3}{5}}5}}{(2^{x}-2^{2})(2^{x}-2^{0})}\leq 0$.

Выражения $(\frac{3}{5})^{x} – 5$, $2^{x}-2^{2}$, $2^{x}-2^{0}$ совпадают по знаку с выражениями $(\frac{3}{5}-1)\cdot (x-log_{\frac{3}{5}}5)$, $(2-1)\cdot (x-2)$ и $(2-1)\cdot (x-0)$ соответственно.

$\frac{(\frac{3}{5}-1)\cdot (x-log_{\frac{3}{5}}5)}{(2-1)\cdot (x-2)\cdot (2-1) \cdot (x-0)} \leq 0$.

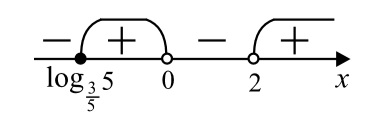
3. $\frac{x-log_{\frac{3}{5}}5}{(x-2)\cdot x} \geq 0$ (см. рис.)

$x \in [log_{\frac{3}{5}} 5;0) \cup (2; +\infty)$.

$\textit {Ответ:}$ $[log_{\frac{3}{5}} 5;0) \cup (2; +\infty)$