ЕГЭ по Математике (профильный)
В окружность вписана трапеция $ABCD$...
Задание:
В окружность вписана трапеция $ABCD$ с основаниями $AD$ и $BC$, один из углов которой равен $60^{\circ}$. В трапецию вписана ещё одна окружность.
а) Докажите, что центр описанной окружности трапеции лежит внутри трапеции.
б) Найдите, во сколько раз $CD$ больше радиуса окружности, касающейся сторон $AB$, $AD$ и вписанной окружности трапеции $ABCD$, если $AD > BC$.
а) Докажите, что центр описанной окружности трапеции лежит внутри трапеции.
б) Найдите, во сколько раз $CD$ больше радиуса окружности, касающейся сторон $AB$, $AD$ и вписанной окружности трапеции $ABCD$, если $AD > BC$.
Решение:
а) План решения.
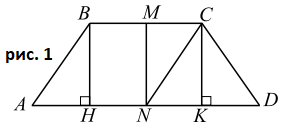
1. Сделаем чертёж (см. рис. 1), считая для определённости, что $AD > BC$ (для пункта a) это не имеет значения).
2. Заметим, что трапеция равнобедренная. Обозначим одну из сторон трапеции какой-либо буквой, выразим остальные стороны.
3. Выразим через ту же букву радиус окружности, описанной около трапеции: это можно сделать но теореме синусов для $\triangle ABD$.
4. Обозначим точкой $N$ середину $AD$, точкой $M$ — середину $BC$. Найдём $CN$.
5. Сравним $CN$ с радиусом описанной окружности. Сделаем вывод, учитывая, что радиус описанной окружности лежит на прямой $MN$.
Решение.
1. Выполним чертёж (см. рис. 1).
2. Так как трапеция $ABCD$ вписана в окружность, то она равнобедренная, то есть $AB = CD = a$. $\angle BAD = 60^{\circ}$. Следовательно, $AH = \frac{1}{2}AB = \frac{1}{2}a$, $KD = \frac{1}{2}a$. Так как в $ABCD$ вписана окружность, то $AB + CD =$ $BC+AD$, отсюда $BC = \frac{1}{2}a$ и $AD = \frac{3}{2}a$.
3. Радиус описанной окружности трапеции $ABCD$ равен радиусу описанной окружности $\triangle ABD$. Из $\triangle ABD$ по теореме синусов $2R = \frac{BD}{sin \angle BAD} =$ $\frac{2}{\sqrt{3}}\cdot \sqrt{BH^{2}+HD^{2}}=$ $\frac{2}{\sqrt{3}}\cdot \sqrt{(\frac{a\sqrt{3}}{2})^{2}+a^{2}} =$ $\frac{\sqrt{7}}{\sqrt{3}}a$, $R=\frac{\sqrt{7}}{2\sqrt{3}}a$.
4. Центр $O$ описанной окружности трапеции $ABCD$ лежит на прямой $MN$, где $M$ и $N$ - середины $BC$ и $AD$ соответственно. $CN = \sqrt{CK^{2}+NK^{2}}=$ $\sqrt{(\frac{a\sqrt{3}}{2})^{2}+(\frac{a}{4})^{2}} = \frac{\sqrt{13}}{4}a$.
5. Сравним $CN$ и $R$, $\frac{\sqrt{13}}{4}>\frac{\sqrt{7}}{2\sqrt{3}}$, то есть $\sqrt{NM^{2}+MC^{2}} > \sqrt{OM^{2}+MC^{2}}$, отсюда $MN > OM$ или радиус описанной окружности лежит на прямой $MN$, а центр описанной окружности лежит внутри отрезка $MN$.
б) План решения.
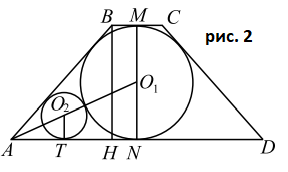
1. Сделаем чертёж (см. рис. 2), обозначив центр вписанной окружности через $O_{1}$ центр второй окружности — через $O_{2}$. Построим радиус $O_{2}T\perp AD$.
2. Из подобных треугольников $O_{2}AT$ и $O_{1}AN$, зная $\angle O_{2}AT$, вычислим $O_{2}T$.
3. Найдём искомое отношение $\frac{CD}{O_{2}T}$
Решение.
1. Выполним чертёж (см. рис. 2).
2. $\triangle O_{2}AT \sim \triangle O_{1}AN$, тогда $\frac{O_{1}N}{O_{2}T} = \frac{AO_{1}}{AO_{2}}$. Обозначим искомый радиус $O_{2}T$ через $x$, получим: $\frac{O_{1}N}{x} = \frac{AO_{1}}{AO_{1}-O_{1}N-x}$. $BH = MN$, из $\triangle ABH:BH =$ $AB \cdot sin60^{\circ}=$ $\frac{a\sqrt{3}}{2}$, $MN = \frac{a\sqrt{3}}{2}$.
Центр окружности, вписанной в угол, лежит на биссектрисе этот угла, поэтому $\angle O_{1}AN =\frac{1}{2}\angle BAD = 30^{\circ}$. Тогда $AO_{1} = 2O_{1}N$ (катет, лежащий против угла в $30^{\circ}$, равен половине гипотенузы). Отсюда $\frac{O_{1}N}{x} = \frac{2O_{1}N}{O_{1}N-x}$, $\frac{1}{x} = \frac{2}{O_{1}N-x}$, $O_{1}N – x = 2x$, $x=\frac{1}{3}O_{1}N =$ $\frac{1}{3}\cdot \frac{1}{2}MN =$ $\frac{1}{6}\cdot \frac{a\sqrt{3}}{2} = \frac{a\sqrt{3}}{12}$, $x=\frac{a\sqrt{3}}{12}$, то есть $O_{2}T = \frac{a\sqrt{3}}{12}$.
3. $\frac{CD}{O_{2}T} = \frac{a}{(\frac{a\sqrt{3}}{12})} = 4\sqrt{3}$.
Ответ: $4\sqrt{3}$.
1. Сделаем чертёж (см. рис. 1), считая для определённости, что $AD > BC$ (для пункта a) это не имеет значения).
2. Заметим, что трапеция равнобедренная. Обозначим одну из сторон трапеции какой-либо буквой, выразим остальные стороны.
3. Выразим через ту же букву радиус окружности, описанной около трапеции: это можно сделать но теореме синусов для $\triangle ABD$.
4. Обозначим точкой $N$ середину $AD$, точкой $M$ — середину $BC$. Найдём $CN$.
5. Сравним $CN$ с радиусом описанной окружности. Сделаем вывод, учитывая, что радиус описанной окружности лежит на прямой $MN$.
Решение.
1. Выполним чертёж (см. рис. 1).
2. Так как трапеция $ABCD$ вписана в окружность, то она равнобедренная, то есть $AB = CD = a$. $\angle BAD = 60^{\circ}$. Следовательно, $AH = \frac{1}{2}AB = \frac{1}{2}a$, $KD = \frac{1}{2}a$. Так как в $ABCD$ вписана окружность, то $AB + CD =$ $BC+AD$, отсюда $BC = \frac{1}{2}a$ и $AD = \frac{3}{2}a$.
3. Радиус описанной окружности трапеции $ABCD$ равен радиусу описанной окружности $\triangle ABD$. Из $\triangle ABD$ по теореме синусов $2R = \frac{BD}{sin \angle BAD} =$ $\frac{2}{\sqrt{3}}\cdot \sqrt{BH^{2}+HD^{2}}=$ $\frac{2}{\sqrt{3}}\cdot \sqrt{(\frac{a\sqrt{3}}{2})^{2}+a^{2}} =$ $\frac{\sqrt{7}}{\sqrt{3}}a$, $R=\frac{\sqrt{7}}{2\sqrt{3}}a$.
4. Центр $O$ описанной окружности трапеции $ABCD$ лежит на прямой $MN$, где $M$ и $N$ - середины $BC$ и $AD$ соответственно. $CN = \sqrt{CK^{2}+NK^{2}}=$ $\sqrt{(\frac{a\sqrt{3}}{2})^{2}+(\frac{a}{4})^{2}} = \frac{\sqrt{13}}{4}a$.
5. Сравним $CN$ и $R$, $\frac{\sqrt{13}}{4}>\frac{\sqrt{7}}{2\sqrt{3}}$, то есть $\sqrt{NM^{2}+MC^{2}} > \sqrt{OM^{2}+MC^{2}}$, отсюда $MN > OM$ или радиус описанной окружности лежит на прямой $MN$, а центр описанной окружности лежит внутри отрезка $MN$.
б) План решения.
1. Сделаем чертёж (см. рис. 2), обозначив центр вписанной окружности через $O_{1}$ центр второй окружности — через $O_{2}$. Построим радиус $O_{2}T\perp AD$.
2. Из подобных треугольников $O_{2}AT$ и $O_{1}AN$, зная $\angle O_{2}AT$, вычислим $O_{2}T$.
3. Найдём искомое отношение $\frac{CD}{O_{2}T}$
Решение.
1. Выполним чертёж (см. рис. 2).
2. $\triangle O_{2}AT \sim \triangle O_{1}AN$, тогда $\frac{O_{1}N}{O_{2}T} = \frac{AO_{1}}{AO_{2}}$. Обозначим искомый радиус $O_{2}T$ через $x$, получим: $\frac{O_{1}N}{x} = \frac{AO_{1}}{AO_{1}-O_{1}N-x}$. $BH = MN$, из $\triangle ABH:BH =$ $AB \cdot sin60^{\circ}=$ $\frac{a\sqrt{3}}{2}$, $MN = \frac{a\sqrt{3}}{2}$.
Центр окружности, вписанной в угол, лежит на биссектрисе этот угла, поэтому $\angle O_{1}AN =\frac{1}{2}\angle BAD = 30^{\circ}$. Тогда $AO_{1} = 2O_{1}N$ (катет, лежащий против угла в $30^{\circ}$, равен половине гипотенузы). Отсюда $\frac{O_{1}N}{x} = \frac{2O_{1}N}{O_{1}N-x}$, $\frac{1}{x} = \frac{2}{O_{1}N-x}$, $O_{1}N – x = 2x$, $x=\frac{1}{3}O_{1}N =$ $\frac{1}{3}\cdot \frac{1}{2}MN =$ $\frac{1}{6}\cdot \frac{a\sqrt{3}}{2} = \frac{a\sqrt{3}}{12}$, $x=\frac{a\sqrt{3}}{12}$, то есть $O_{2}T = \frac{a\sqrt{3}}{12}$.
3. $\frac{CD}{O_{2}T} = \frac{a}{(\frac{a\sqrt{3}}{12})} = 4\sqrt{3}$.
Ответ: $4\sqrt{3}$.
Задание добавил(а)
Моя страничка ВКонтакте: vk.com/id64028587
О задание:
Источник условия: Книга: Математика. Подготовка к ЕГЭ-2017. Профильный уровень. 40 тренировочных вариантов. Под редакцией Ф.Ф. Лысенко, С.Ю. Калабухова.
Источник решения: Книга: Решение заданий из книги указанной в источнике условия. Автор неизвестен.
Источник решения: Книга: Решение заданий из книги указанной в источнике условия. Автор неизвестен.
Обсуждения
Только зарегистрированные пользователи могут оставлять комментарии.

