Найдите все значения параметра $a$,...

Найдите все значения параметра $a$, при каждом из которых решение неравенства $\frac{(2\sqrt{x}-a)(a-x)}{\sqrt{3-a^{2}-x^{2}}} \geq 0$ отрезок длины не менее $0,5$.

$\frac{(2\sqrt{x}-a)(a-x)}{\sqrt{3-a^{2}-x^{2}}} \geq 0$. Попробуем преобразовать неравенство к более простому виду. Заметим, что знаменатель влияет только на ОДЗ. Поэтому неравенство равносильно системе $\small \begin{cases} (2\sqrt{x}-a)(a-x)\geq 0, \\ 3-a^{2}-x^{2}>0 \end{cases}$. Второе неравенство системы преобразуем так, чтобы получить неравенство для внутренней части круга. Первое неравенство преобразуем так, чтобы скобки выглядели симметрично $\small \begin{cases} (2\sqrt{x}-a)(x-a)\leq 0 \\ a^{2}+x^{2}<3 \end{cases}$ $(*)$

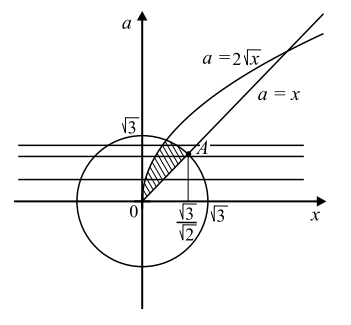
Изобразим множество решений системы $(*)$ в системе координат $Oxa$ (см. рис.). Решению соответствует заштрихованная область. При этом каждому фиксированному значению $a$ соответствует горизонтальная прямая. При фиксированном значении $a$ решениями системы $(*)$ будут $x$, равные абсциссам тех точек горизонтальной прямой, которые лежат в заштрихованной области.

Прямая $a=x$ пересекает окружность $x^{2}+a^{2}=3$ при $a=x=\frac{\sqrt{3}}{\sqrt{2}}$.

1) Из рисунка видно, что если горизонтальная прямая $a=a_{0}$ лежит ниже (не выше) точки $A$, то отрезок этой прямой в заштрихованной области идёт от графика $a=2\sqrt{x}$ до графика $a=x$.

2) Если же горизонтальная прямая $a=a_{0}$ лежит выше точки $A$, то отрезок этой прямой в заштрихованной области идёт от графика $a=2\sqrt{x}$ до окружности $a^{2}+x^{2}=3$, при этом точки самой окружности в заштрихованную область не входят.

Таким образом, в первом случае $($то есть при и $a\leq \frac{\sqrt{3}}{\sqrt{2}}$$)$ выполняется $a\leq 2\sqrt{x}$, $a\geq x$,
следовательно, $x \in [\frac{a^{2}}{4};a]$.

При $a> \frac{\sqrt{3}}{\sqrt{2}}$ решением является промежуток $[\frac{a^{2}}{4};\sqrt{3-a^{2}})$.

Отсюда решение содержит отрезок длиной не менее $\frac{1}{2}$, если

$\left[
\begin{gathered}
\small \begin{cases} a\leq \frac{\sqrt{3}}{\sqrt{2}}, \\ a-\frac{1}{4}a^{2}\geq 0,5, \end{cases} \\
\small \begin{cases} a>\frac{\sqrt{3}}{\sqrt{2}}, \\ \sqrt{3-a^{2}}-\frac{a^{2}}{4}> 0,5; \end{cases}\\
\end{gathered}
\right.$

$\left[
\begin{gathered}
\small \begin{cases} a\leq \frac{\sqrt{3}}{\sqrt{2}}, \\ a^{2}-4a+2\leq 0, \end{cases} \\
\small \begin{cases} a> \frac{\sqrt{3}}{\sqrt{2}} \\ 3-a^{2}>(\frac{a^{2}}{4}+\frac{1}{2})^{2}. \end{cases}\\
\end{gathered}
\right.$

Решив системы, получим: $a \in [2-\sqrt{2};\frac{\sqrt{3}}{\sqrt{2}}]$ или $a \in (\frac{\sqrt{3}}{\sqrt{2}}; \sqrt{2})$, отсюда $a \in [2 - \sqrt{2}; \sqrt{2})$.

Замечание. Задачу можно решить и другими способами, например аналитически. Получив систему $(*)$, можно заметить, что первое неравенство системы при $a<0$ не имеет решений, а при $a\geq 0$ имеет решением промежуток $[\frac{1}{4}a^{2};a]$ (если $a\leq 4$) или промежуток $[a;\frac{1}{4}a^{2}]$ (если $a>4$). Решением второго неравенства будут $x$, удовлетворяющие неравенству $x < \sqrt{3-a^{2}}$. Отсюда, в частности, $a\leq \sqrt{3}$, то есть случай $a>4$ не возможен.

Несложно убедиться, что при ограничениях $0\leq a \leq \sqrt{3}$ для решения задачи достаточно решить систему

$\small \begin{cases} a-\frac{1}{4}a^{2}\geq 0,5, \\ \sqrt{3-a^{3}}-\frac{a^{2}}{4}>0,5. \end{cases}$

Ответ: $a \in [2-\sqrt{2};\sqrt{2})$.