На рисунке изображён график функции...

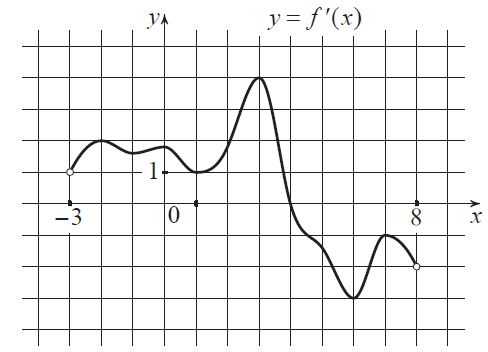
На рисунке изображён график функции $y=f'(x)$ - производной функции $f(x)$, определенной на интервале (-3; 8). В какой точке отрезка [-2; 4] функция $f(x)$ принимает наибольшее значение?

У нас задан график производной, значит на заданном интервале нужно найти точку пересечения с осью абсцисс (ось Ох). Если график расположен выше оси Ох, то знак производной будет положительным, т.е. функция будет возрастать. Если график расположен ниже оси Ох, то знак производной будет отрицательным (функция убывает).

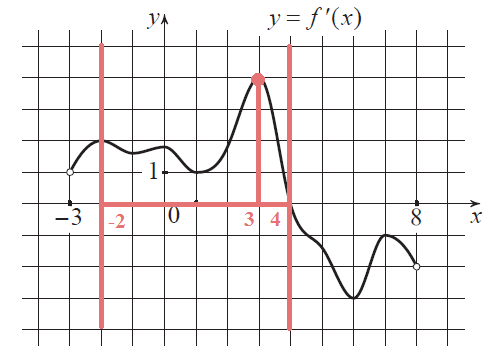
На отрезке [-2; 4] график производной выше оси Ox, поэтому функция на этом отрезке является возрастающей. По графику видно, что наибольшее значение будет в точке х=3.