ЕГЭ по Математике (профильный)
Найдите объем многогранника,...
Задание:
Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
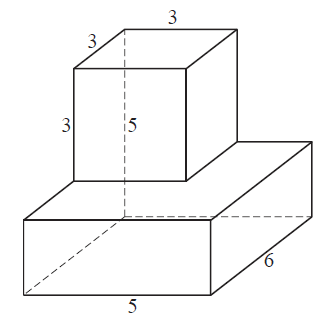
Решение:
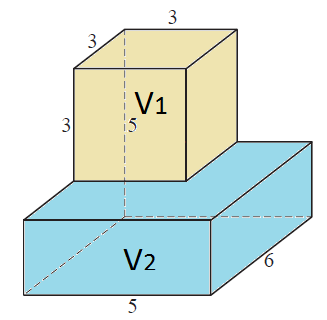
Многогранник состоит из куба $V_{1}$ и прямоугольного параллелепипеда $V_{2}$ (смотреть рисунок). Объем - сумма этих двух фигур.
Объемы этих фигур легко посчитать, зная их длину, ширину и высоту, так как формула для нахождения объеме прямоугольного параллелепипеда $V=a\cdot b\cdot h$; а для куба $V=a\cdot a\cdot a$, так как у куба все стороны равны.
Объём куба будет равен $V_{1}=3\cdot 3\cdot 3=27$. У прямоугольного параллелепипеда неизвестна высота, найдем её: высота куба с параллелепипедом равна 5, а высота куба равна 3, значит, чтобы найти высоту параллелепипеда нужно из высота куба с параллелепипедом вычесть высоту куба, т.е. 5-3=2. Найдем объём прямоугольного параллелепипеда $V_{2}=6\cdot 5\cdot 2=60$.
Значит, объём многогранника будет равен $V=V_{1}+V_{2}=60+27=87$.
Объемы этих фигур легко посчитать, зная их длину, ширину и высоту, так как формула для нахождения объеме прямоугольного параллелепипеда $V=a\cdot b\cdot h$; а для куба $V=a\cdot a\cdot a$, так как у куба все стороны равны.
Объём куба будет равен $V_{1}=3\cdot 3\cdot 3=27$. У прямоугольного параллелепипеда неизвестна высота, найдем её: высота куба с параллелепипедом равна 5, а высота куба равна 3, значит, чтобы найти высоту параллелепипеда нужно из высота куба с параллелепипедом вычесть высоту куба, т.е. 5-3=2. Найдем объём прямоугольного параллелепипеда $V_{2}=6\cdot 5\cdot 2=60$.
Значит, объём многогранника будет равен $V=V_{1}+V_{2}=60+27=87$.
Ответ:
87
Задание добавил(а)
Редактор проекта ExamMe
О задание:
Источник условия: Книга: Подготовка к ЕГЭ. Диагностические работы. ЕГЭ 2017. Профильный уровень. Издательство: МЦНМО, 2017
Источник решения: Авторский коллектив ExamMe.RU
Источник решения: Авторский коллектив ExamMe.RU
Обсуждения
Только зарегистрированные пользователи могут оставлять комментарии.
