ЕГЭ по Математике (профильный)
На клетчатой бумаге в размером 1 х 1...
Задание:
На клетчатой бумаге в размером 1 х 1 изображён равнобедренный прямоугольный треугольник. Найдите длину его медианы, проведенной к гипотенузе.
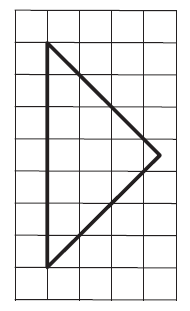
Решение:
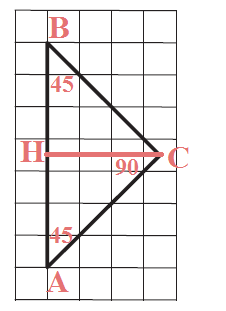
По условию, треугольник ABC является равнобедренным и прямоугольным, значит углы при основании равны и один угол равен 90 градусов. Мы знаем, что в треугольнике сумма углов равна 180 градусов, а т.к. один угол известен и составляет 90 градусов, то два других угла будут равны $180^{\circ}-90^{\circ}=90^{\circ}$. Значит, углы при основании треугольника будут равны по $90^{\circ}\div 2=45^{\circ}$.
Одно из свойств равнобедренного треугольника гласит - в равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой. В нашем случае НС является и медианой и биссектрисой, а значит делит прямой угол пополам.
По клеткам видно, что гипотенуза АВ = 7, значит медиана НС = $7\div 2=3,5.$
Одно из свойств равнобедренного треугольника гласит - в равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой. В нашем случае НС является и медианой и биссектрисой, а значит делит прямой угол пополам.
По клеткам видно, что гипотенуза АВ = 7, значит медиана НС = $7\div 2=3,5.$
Ответ:
3,5
Задание добавил(а)
Редактор проекта ExamMe
О задание:
Источник условия: Книга: Подготовка к ЕГЭ. Диагностические работы. ЕГЭ 2017. Профильный уровень. Издательство: МЦНМО, 2017
Источник решения: Авторский коллектив ExamMe.RU
Источник решения: Авторский коллектив ExamMe.RU
Обсуждения
Только зарегистрированные пользователи могут оставлять комментарии.
