Основание равнобедренной трапеции...

Основание равнобедренной трапеции равны 12 и 18, а её периметр равен 40. Найдите площадь трапеции.

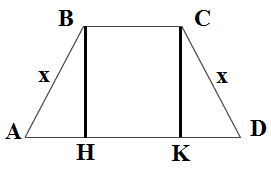
Трапеция у нас равнобедренная, значит у неё боковые стороны равны, т.е. AB = CD (см. рисунок ниже).

Периметр - это сумма всех сторон. Пусть, x - боковая сторона трапеции, значит, периметр трапеции будет равен $P=AB+CD+BC+AD=x+x+BC+AD.$ Подставим численные значения и найдем оттуда боковую сторону трапеции:
\[40=x+x+12+18\]
\[2x=10\]
\[x=5.\]

Площадь равнобедренной трапеции находится по формуле $S=\frac{a+b}{2}\cdot h=\frac{BC+AD}{2}\cdot BH.$ В данной формуле нам неизвестна только высота, найдем её из прямоугольного треугольника ABH по теореме Пифагора:
\[AB^{2}=BH^{2}+AH^{2}\]

Найдем сторону $AH=KD=\frac{18-12}{2}=3$ и подставим значения в теорему Пифагора:
\[5^{2}=BH^{2}+3^{2}\]
\[BH^{2}=16\]
\[BH=4.\]

Подставим численные значения в формулу для нахождения площади:
\[S=\frac{18+12}{2}\cdot 4=60.\]