а) Решите уравнение $1-cos^{2}x =...

а) Решите уравнение $1-cos^{2}x = sin (\pi – x)$.

б) Найдите корни уравнения, принадлежащие промежутку $[\frac{9\pi}{2};\frac{13\pi}{2})$.

а) Используя формулы приведения и основное тригонометрическое тождество, преобразуем уравнение так, чтобы в нём была только одна тригонометрическая функция (синус) с одинаковым аргументом $(x)$. Сделав замену $sinx=t$, получим квадратное уравнение, решив которое вернёмся к переменной $x$.

$1-2(1-sin^{2}x)-sin(\pi – x) = 0$, $2sin^{2}x – sinx – 1= 0$.

Пусть $sinx = t$, тогда $2t^{2}-t-1=0$, $t_{1} = 1$, $t_{2} = -\frac{1}{2}$.

$sinx = 1$, тогда $x = \frac{\pi}{2} + 2\pi k$, $k \in Z$,

$sinx = -\frac{1}{2}$, тогда $x=(-1)^{n+1}\frac{\pi}{6}+\pi n$, $n \in Z$.

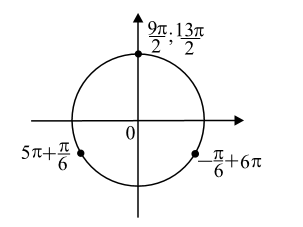
б) Корни, принадлежащие промежутку $[\frac{9\pi}{2}; \frac{13\pi}{2})$, найдём с помощью тригонометрической окружности (см. рис.).

$\frac{9\pi}{2} \in [\frac{9\pi}{2}; \frac{13\pi}{2})$;

$5\pi + \frac{\pi}{6} = \frac{31\pi}{6}$;

$6\pi - \frac{\pi}{6} = \frac{35\pi}{6}$;

Ответ: а) $\frac{\pi}{2} + 2\pi k$, $k \in Z$, $(-1)^{n+1}\frac{\pi}{6} + \pi n$, $n \in Z$; б) $\frac{9\pi}{2}$, $\frac{31\pi}{6}$, $\frac{35\pi}{6}$.