Основанием прямой призмы...

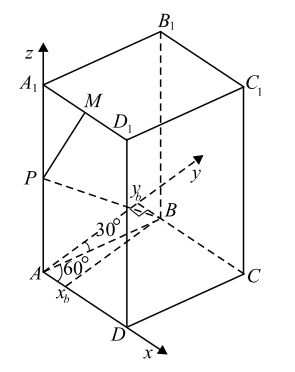
Основанием прямой призмы $ADCA_{1}B_{1}C_{1}D_{1}$ является ромб с острым углом $A$, равным $60^{\circ}$. Все рёбра этой призмы равны $8$. Точки $P$ и $M$ — середины рёбер $AA_{1}$ и $A_{1}D_{1}$ соответственно.

а) Докажите, что прямые $PB$ и $PM$ перпендикулярны.

б) Найдите угол между плоскостями $PMB$ и $AA_{1}D$.

а) Будем использовать метод координат. Найдем скалярное произведение векторов $\vec{PB}$ и $\vec{PM}$, а затем косинус угла между этими векторами. Выберем систему координат. Направим ось $Ox$ вдоль $AD$, ось $Oz$ вдоль $AA_{1}$ и ось $Oy \perp AD$ в плоскости $ABC$ (см. рис.). $A$ — начало координат.

Тогда $A(0;0;0)$; $A_{1}(0;0;8)$; $P(0;0;4)$; $M(4;0;8)$;

$B(BAcos60^{\circ};BAsin60^{\circ};0)$, то есть $B(4;4\sqrt{3};0)$, $B_{1}(4;4\sqrt{3};8)$.

Найдём координаты векторов: $\vec{PM} = \begin{Bmatrix}4;0;4\end{Bmatrix}$; $\vec{PB} = \begin{Bmatrix}4;4\sqrt{3};-4\end{Bmatrix}$.

Пусть угол между $\vec{PM}$ и $\vec{PB}$ равен $a$.

Получаем: $cos a = \frac{\vec{PM}\cdot \vec{PB}}{|\vec{PM}\cdot \vec{PB}|} =$ $\frac{4\cdot 4 + 0\cdot 4\sqrt{3}-4\cdot 4}{|\vec{PM}| \cdot |\vec{PB}|} = 0$.

$cosa = 0$, значит, $\vec{PM} \perp \vec{PB}$ и прямые $PM$ и $PB$ перпендикулярны.

б) Угол между плоскостями равен углу между ненулевыми векторами, перпендикулярными этим плоскостям (или, если угол тупой, смежному с ним углу). Такие вектора называют нормалями к плоскостям. Найдём их. Пусть $\vec{n_{1}} = \begin{Bmatrix}x;y;z\end{Bmatrix}$ перпендикулярен плоскости $PMB$. Найдём его, решив систему $\small \begin{cases} \vec{n_{1}} \perp \vec{PM}, \\ \vec{n_{1}} \perp \vec{PB}. \end{cases}$

$\small \begin{cases} \vec{n_{1}} \cdot \vec{PM} = 0, \\ \vec{n_{1}}\cdot \vec{PB} = 0; \end{cases}$ $\small \begin{cases} 4x+0y+4z=0, \\ 4x+4\sqrt{3y} - 4z = 0; \end{cases}$ $\small \begin{cases} z=-x, \\ y=\frac{-2x}{\sqrt{3}}. \end{cases}$

Возьмём $x=1$; $y=\frac{-2}{\sqrt{3}}$; $z=-1$. $\vec{n_{1}} = \begin{Bmatrix}1;\frac{-2}{\sqrt{3}}; -1\end{Bmatrix}$.

Пусть $\vec{n_{2}} = \begin{Bmatrix}x;y;z\end{Bmatrix}$ перпендикулярен плоскости $AA_{1}D$. Найдём его, решив систему

$\small \begin{cases} \vec{n_{2}} \perp \vec{AA_{1}}, \\ \vec{n_{2}} \perp \vec{AD}. \end{cases}$ $\small \begin{cases} 0x+0y+8z=0, \\ 8x+0y+0z=0; \end{cases}$ $\small \begin{cases} z=0, \\ x=0. \end{cases}$

Возьмём $x=0$; $y=1$; $z=0$. $\vec{n_{2}} = \begin{Bmatrix}0;1;0\end{Bmatrix}$.

Найдём косинус искомого угла $\beta$ (он равен модулю косинуса угла между $\vec{n_{1}}$ и $\vec{n_{2}}$).

$cos \beta = \frac{|\vec{n_{1}}\cdot \vec{n_{2}}|}{|\vec{n_{1}}|\cdot |\vec{n_{2}}|} =$ $\frac{|1\cdot 0 - \frac{2}{\sqrt{3}}\cdot 1 - 1 \cdot 0|}{\sqrt{1^{2}+(-\frac{2}{\sqrt{3}})^{2}+1^{2}}\cdot \sqrt{0^{2}+1^{2}+0^{2}}} =$ $\frac{\frac{2}{\sqrt{3}}}{\sqrt{\frac{10}{3}}} = $ $\frac{2}{\sqrt{10}} = \frac{\sqrt{10}}{5}$.

$cos \beta = \frac{\sqrt{10}}{5}$, $\beta = arccos \frac{\sqrt{10}}{5}$.

Ответ: $arccos \frac{\sqrt{10}}{5}$.