ЕГЭ по Математике (профильный)
Решите неравенство...
Задание:
Решите неравенство $6^{x}\sqrt{15-x^{2}-2x} \geq$ $36\sqrt{15-x^{2}-2x}$.
Решение:
Будем использовать метод интервалов, предварительно найдя ОДЗ и нули левой части неравенства. Преобразуем неравенство.
$(6^{x}-36) \sqrt{15-x^{2}-2x}\geq 0$.
Найдём ОДЗ неравенства:
$-x^{2}-2x+15\geq 0$; $x^{2}+2x-15\leq 0$; $(x-3)(x+5)\leq 0$, $x \in [-5;3]$.
Выражение $\sqrt{15-x^{2}-2x}$ неотрицательно при любом допустимом значении $x$, значит неравенство выполняется при $6^{x}\geq 36$, $6^{x}\geq 6^{2}$, $x\geq 2$, а также если $\sqrt{15-x^{2}-2x} = 0$; $x^{2}+2x-15=0$; $x_{1}=-5$, $x_{2}=3$.
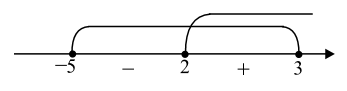
Учтём ОДЗ (см.рис.) и найдём знаки левой части неравенства.
$x \in [2;3] \cup \begin{Bmatrix}-5\end{Bmatrix}$.
Ответ: $[2;3] \cup \begin{Bmatrix}-5\end{Bmatrix}$.
$(6^{x}-36) \sqrt{15-x^{2}-2x}\geq 0$.
Найдём ОДЗ неравенства:
$-x^{2}-2x+15\geq 0$; $x^{2}+2x-15\leq 0$; $(x-3)(x+5)\leq 0$, $x \in [-5;3]$.
Выражение $\sqrt{15-x^{2}-2x}$ неотрицательно при любом допустимом значении $x$, значит неравенство выполняется при $6^{x}\geq 36$, $6^{x}\geq 6^{2}$, $x\geq 2$, а также если $\sqrt{15-x^{2}-2x} = 0$; $x^{2}+2x-15=0$; $x_{1}=-5$, $x_{2}=3$.
Учтём ОДЗ (см.рис.) и найдём знаки левой части неравенства.
$x \in [2;3] \cup \begin{Bmatrix}-5\end{Bmatrix}$.
Ответ: $[2;3] \cup \begin{Bmatrix}-5\end{Bmatrix}$.
Задание добавил(а)
Моя страничка ВКонтакте: vk.com/id64028587
О задание:
Источник условия: Книга: Математика. Подготовка к ЕГЭ-2017. Профильный уровень. 40 тренировочных вариантов. Под редакцией Ф.Ф. Лысенко, С.Ю. Калабухова.
Источник решения: Книга: Решение заданий из книги указанной в источнике условия. Автор неизвестен.
Источник решения: Книга: Решение заданий из книги указанной в источнике условия. Автор неизвестен.
Обсуждения
Только зарегистрированные пользователи могут оставлять комментарии.

