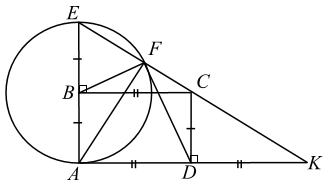
$ABCD$ — прямоугольник. Окружность с...

$ABCD$ — прямоугольник. Окружность с центром в точке $B$ радиусом $AB$ пересекает продолжение стороны $AB$ в точке $E$. Прямая $EC$ пересекает прямую $AD$ в точке $K$, а окружность во второй раз — в точке $F$.

а) Докажите, что $DK = DF$.

б) Найдите $KC$, если $BF = 20$, $DF = 21$.

а) Докажем, что $AF \perp EK$ и $AD = DK$, а затем воспользуемся свойством медианы $FD$ прямоугольного треугольника $AFK$. $ABCD$— прямоугольник, поэтому его углы прямые и $CB=AD$, $CD=AB$. $\angle EBC = \angle CDK = 90^{\circ}$(см. рис.).

$BE = BA$ как радиусы окружности. Получаем, что $BE = CD$.

$\angle BEC = \angle DCK$ как соответственные углы при $AB \parallel CD$ (секущая $EK$).

$\triangle BEC = \triangle DCK$ (по стороне и двум прилежащим к ней углам), значит, $BC = KD$. Но $BC = AD$, из этого получаем: $AD = DK$.

Проведём $AF$. $\angle AFE$ — вписанный, он опирается на диаметр, значит, $\angle AFE$ прямой.

$\angle AFK = \angle 180^{\circ} - \angle AFE = 90 ^{\circ}$. В прямоугольном треугольнике $AFK$ медиана $FD$ равна половине гипотенузы $AK$, значит, $FD=AD=DK$.

б) Воспользуемся теоремой Пифагора для треугольника $CDK$. $BF = AB = 20$ (радиусы), $AB=CD = 20$. $DF = DK = 21$ (см. пункт $a$)).

По теореме Пифагора $CK^{2} = CD^{2}+DK^{2} = 20^{2}+ 21^{2}$, $CK = 29$.

Ответ: $29$.