Найдите, при каких значениях...

Найдите, при каких значениях параметра $a$ система

$\small \begin{cases} x^{2}+y^{2}+84 = a^{2}+18x,\\ ||x-8|-|x-6||=y \end{cases}$ имеет не менее трёх решений.

В осях $Oxy$ построим графики обоих уравнений для некоторых значений $a$. Заметим, что первое уравнение задаёт окружность, а для второго построим сначала график функции без внешнего модуля. Проанализируем, как изменяются графики в зависимости от $a$, и определим, в каких ситуациях графики пересекаются ровно в $3$ точках. Найдём граничные значения $a$.

Построим графики уравнений системы.

1) Преобразуем уравнение $x^{2}+y^{2}+84 = a^{2}+18x$.
$x^{2}-18x + 81 + y^{2} + 84 = a^{2}+ 81$, $(x-9)^{2}+y^{2} = a^{2} – 3$. При $a^{2}-3 > 0$ это окружность с центром $(9;0)$ и радиусом $R = \sqrt{a^{2}-3}$. При $a^{2}=3$ система несовместна (решение первого уравнения – пара $(9;0)$, эта пара не является решением второго уравнения).

2) $||x-8| - |x-6|| = y$.

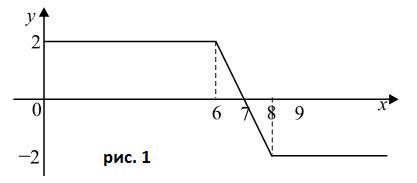
Построим сначала график уравнения $y = |x-8| - |x-6|$ (см. рис. 1)

При $x\leq 6$ $y=-x+8+x-6$, $y = 2$.

При $6< x \leq 8$ $y = -x+8 – x+6$, $y=-2x+14$.

При $x>8$ $y=x-8-x+6$, $y=-2$.

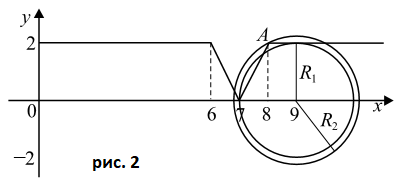
Отразим ту часть графика, где $y<0$, относительно оси $Ox$ и получим график $y=||x-8|-|x-6||$ (см. рис. 2).

3) Система имеет не менее $3$ решений, если графики имеют не менее $3$ точек пересечения. По рисунку видно, что это выполняется при $R_{1}\leq R \leq R_{2}$. При $R = R_{1}$ окружность касается прямой $y=2$, $R_{1}=2$. $R=R_{2}$ — радиус окружности, которая проходит через точку $A(8;2)$. Найдём $R_{2}$.

$(x-9)^{2} + y^{2} = R_{2}^{2}$, $(8-9)^{2} + 2^{2} = R_{2}^{2}$, $R_{2} = \sqrt{5}$.

Получим: $2\leq R \leq \sqrt{5}$, $2 \leq \sqrt{a^{2}-3} \leq \sqrt{5}$, $4\leq a^{2}-3 \leq 5$, $7 \leq a^{2} \leq 8$, $\sqrt{7} \leq |a| \leq 2\sqrt{2}$. $a \in [-2\sqrt{2}; - \sqrt{7}] \cup [\sqrt{7};2\sqrt{2}]$.

Ответ: $[-2\sqrt{2}; - \sqrt{7}] \cup [\sqrt{7};2\sqrt{2}]$.