ЕГЭ по Математике (профильный)
Найдите наибольшее значение функции...
Задание:
Найдите наибольшее значение функции $y=ln(x+4)^{9}-9x$ на отрезке $[-3,5; 0].$
Решение:
Для начала найдем производную функции, пользуясь правилами нахождения производных:
\[(Cx)'=C\]
\[(lnx)'=\frac{1}{x}\]
Получим:
\[y'=\frac{1}{(x+4)^{9}}\cdot 9\cdot (x+4)^{8}-9=\frac{9}{x+4}-9.\]
Приравняем производную к нулю:
\[\frac{9}{x+4}-9=0\]
\[9-9x-36=0\]
\[-9x=27\]
\[x=-3.\]
Данная точка принадлежит промежутку $[-3,5; 0]$. Отметим точки -3,5; -3 и 0 на числовой прямой и расставим знаки производной функции на получившихся промежутках, подставляя любые значения из промежутков в найденную производную (см. рисунок ниже).
В точке х = -3 производная функции меняет знак с положительного на отрицательный, значит это искомая точка максимума. Найдем значение функции при x = -3:
\[y(-3,2)=ln(-3+4)^9-9\cdot (-3)=ln1+27=27.\]
Так же можно найти наибольшее значение функции, вычислив значения в точке x = -3 и в граничных точках.
\[(Cx)'=C\]
\[(lnx)'=\frac{1}{x}\]
Получим:
\[y'=\frac{1}{(x+4)^{9}}\cdot 9\cdot (x+4)^{8}-9=\frac{9}{x+4}-9.\]
Приравняем производную к нулю:
\[\frac{9}{x+4}-9=0\]
\[9-9x-36=0\]
\[-9x=27\]
\[x=-3.\]
Данная точка принадлежит промежутку $[-3,5; 0]$. Отметим точки -3,5; -3 и 0 на числовой прямой и расставим знаки производной функции на получившихся промежутках, подставляя любые значения из промежутков в найденную производную (см. рисунок ниже).
В точке х = -3 производная функции меняет знак с положительного на отрицательный, значит это искомая точка максимума. Найдем значение функции при x = -3:
\[y(-3,2)=ln(-3+4)^9-9\cdot (-3)=ln1+27=27.\]
Так же можно найти наибольшее значение функции, вычислив значения в точке x = -3 и в граничных точках.
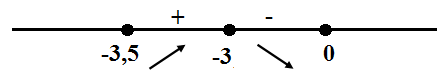
Ответ:
27
Задание добавил(а)
Редактор проекта ExamMe
О задание:
Источник условия: Книга: Подготовка к ЕГЭ. Диагностические работы. ЕГЭ 2017. Профильный уровень. Издательство: МЦНМО, 2017
Источник решения: Авторский коллектив ExamMe.RU
Источник решения: Авторский коллектив ExamMe.RU
Обсуждения
Только зарегистрированные пользователи могут оставлять комментарии.
