ЕГЭ по Математике (профильный)
В треугольнике $ABC$ угол $C$ равен...
Задание:
В треугольнике $ABC$ угол $C$ равен $90^{\circ}$, $BC = 18$, $cos A = \frac{5\sqrt{26}}{26}$. Найдите $AC$.
Решение:
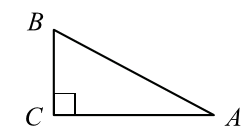
$cos A = \frac{5\sqrt{26}}{26} =$ $\frac{5}{\sqrt{26}}$. В прямоугольном треугольнике с острым углом $A$ (см. рис.)
$sin A = \sqrt{1-cos^{2}A} =$ $\sqrt{1-\frac{25}{26}} = \frac{1}{\sqrt{26}}$.
$tg A = \frac{sinA}{cosA} = \frac{1}{5}$. $tgA = \frac{BC}{AC}$, $\frac{18}{AC}=\frac{1}{5}$, $AC = 18 : \frac{1}{5} = 90$.
$sin A = \sqrt{1-cos^{2}A} =$ $\sqrt{1-\frac{25}{26}} = \frac{1}{\sqrt{26}}$.
$tg A = \frac{sinA}{cosA} = \frac{1}{5}$. $tgA = \frac{BC}{AC}$, $\frac{18}{AC}=\frac{1}{5}$, $AC = 18 : \frac{1}{5} = 90$.
Ответ:
90
Задание добавил(а)
Моя страничка ВКонтакте: vk.com/id64028587
О задание:
Источник условия: Книга: Математика. Подготовка к ЕГЭ-2017. Профильный уровень. 40 тренировочных вариантов. Под редакцией Ф.Ф. Лысенко, С.Ю. Калабухова.
Источник решения: Книга: Решение заданий из книги указанной в источнике условия. Автор неизвестен.
Источник решения: Книга: Решение заданий из книги указанной в источнике условия. Автор неизвестен.
Обсуждения
Только зарегистрированные пользователи могут оставлять комментарии.

