ЕГЭ по Математике (профильный)
Найдите длину диагонали...
Задание:
Найдите длину диагонали прямоугольника, вершины которого имеют координаты $(2; 1), (2; 4), (6; 1), (6; 4)$.
Решение:
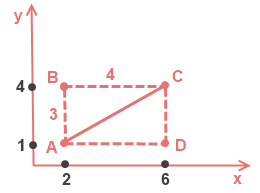
Для наглядности начертим и обозначим вершины этого прямоугольника (см. рисунок). А(2; 1), B(2; 4), D(6; 1), C(6; 4).
Найдем длину стороны $AB = 4-1 = 3$
Найдем длину стороны $BC = 6-2 = 4$
По теореме Пифагора вычислим диагональ AC.
\[AC^2=AB^2+BC^2\]\[AC=\sqrt{3^2+4^2}\]\[AC=\sqrt{9+16}=\sqrt{25}=5\]
Найдем длину стороны $AB = 4-1 = 3$
Найдем длину стороны $BC = 6-2 = 4$
По теореме Пифагора вычислим диагональ AC.
\[AC^2=AB^2+BC^2\]\[AC=\sqrt{3^2+4^2}\]\[AC=\sqrt{9+16}=\sqrt{25}=5\]
Ответ:
5
Задание добавил(а)
Создатель и главный администратор проекта ExamMe.
О задание:
Источник условия: Книга: Подготовка к ЕГЭ. Диагностические работы. ЕГЭ 2017. Профильный уровень. Издательство: МЦНМО, 2017
Источник решения: Авторский коллектив ExamMe.RU
Источник решения: Авторский коллектив ExamMe.RU
Обсуждения
Только зарегистрированные пользователи могут оставлять комментарии.
