ЕГЭ по Математике (профильный)
Дана равнобедренная трапеция $ABCD$...
Задание:
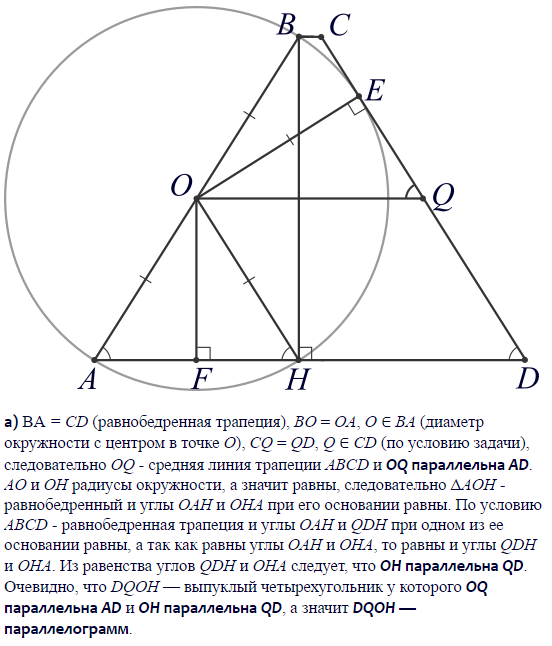
Дана равнобедренная трапеция $ABCD$ с основаниями $AD$ и $BC$. Окружность с центром $O$, построенная на боковой стороне $AB$ как на диаметре, касается боковой стороны $CD$ и второй раз пересекает большее основание $AD$ в точке $H$, точка $Q$ — середина $CD$.
а) Докажите, что четырёхугольник $DQOH$ — параллелограмм.
б) Найдите $AD$, если $\angle BAD = 67,5°$ и $BC = 3$.
а) Докажите, что четырёхугольник $DQOH$ — параллелограмм.
б) Найдите $AD$, если $\angle BAD = 67,5°$ и $BC = 3$.
Решение:


Задание добавил(а)
Создатель и главный администратор проекта ExamMe.
О задание:
Источник условия: fipi.ru
Источник решения: studymath.my-solutions.ru
Источник решения: studymath.my-solutions.ru
Обсуждения
Только зарегистрированные пользователи могут оставлять комментарии.
