ЕГЭ по Математике (профильный)
Прямая, проходящая через середину...
Задание:
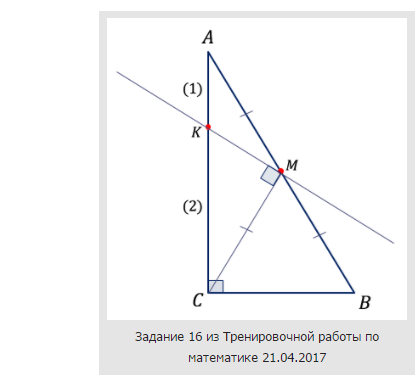
Прямая, проходящая через середину $M$ гипотенузы $AB$ прямоугольного треугольника $ABC$, перпендикулярна $CM$ и пересекает катет $AC$ в точке $K$. При этом $AK:KC=1:2$.
а) Докажите, что $\angle BAC = 30^{\circ}$
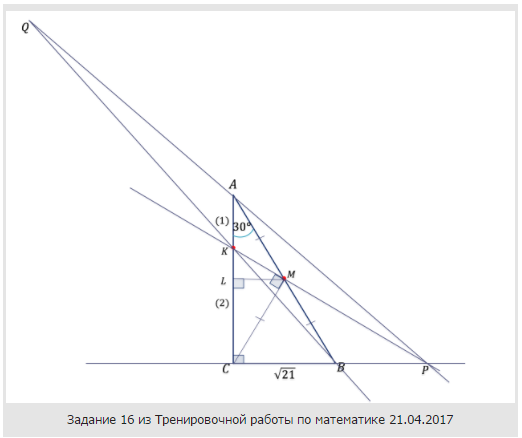
б) Пусть прямые $MK$ и $BC$ пересекается в точке $P$, а прямые $AP$ и $BK$ - в точке $Q$. Найдите $KQ$, если $BC=\sqrt{21}$
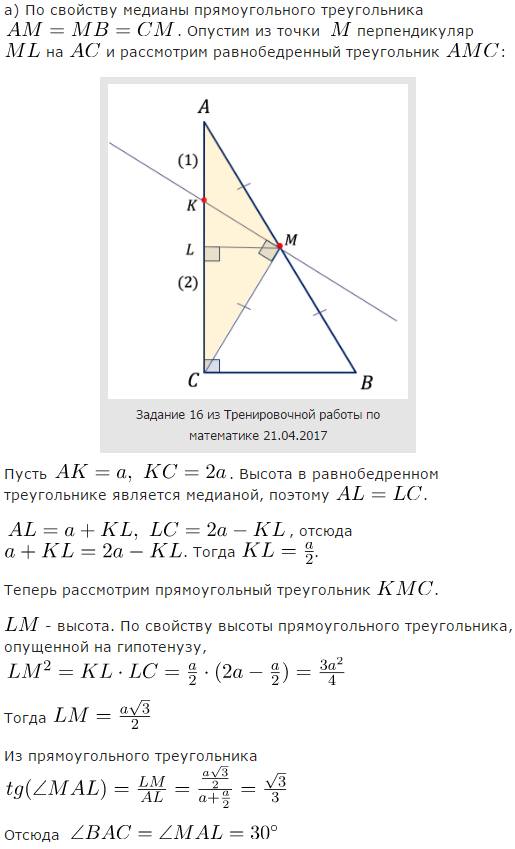
а) Докажите, что $\angle BAC = 30^{\circ}$
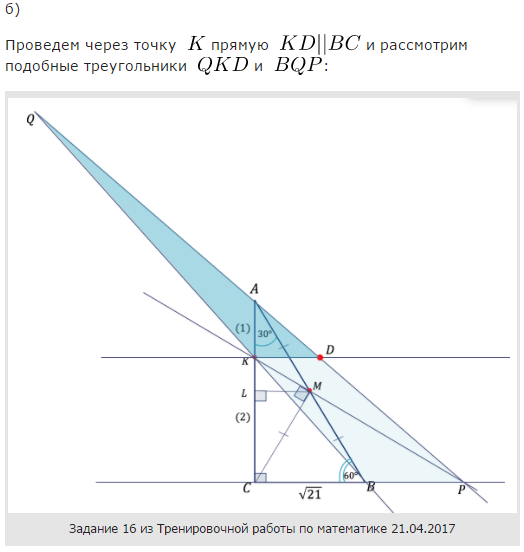
б) Пусть прямые $MK$ и $BC$ пересекается в точке $P$, а прямые $AP$ и $BK$ - в точке $Q$. Найдите $KQ$, если $BC=\sqrt{21}$
Решение:

Задание добавил(а)
Создатель и главный администратор проекта ExamMe.
О задание:
Источник условия: Тренировочная работа 21.04.2017
Источник решения: И.В. Фельдман, репетитор по математике (ege-ok.ru)
Источник решения: И.В. Фельдман, репетитор по математике (ege-ok.ru)
Обсуждения
Только зарегистрированные пользователи могут оставлять комментарии.
*..что QB и AC есть..
camera_alt


Наверное, можно достроить QC и потом заметить, что QB делит AC в отношении 2:1. Из этого, думаю, следует, что QB и AB есть медианы QCP. А тогда QK=2KB=14.
camera_alt

