ЕГЭ по Математике (профильный)
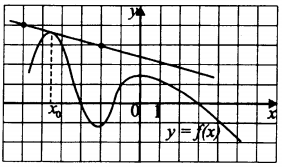
На рисунке изображён график функции...
Задание:
На рисунке изображён график функции $y = f(x)$ и касательная к нему в точке с абсциссой $x_{0}$. Найдите значение производной функции $f(x)$ в точке $x_{0}$.
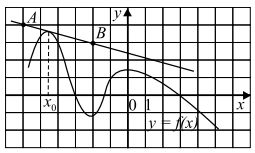
Решение:
По рисунку определяем, что касательная проходит через точки $A(-6; 4)$ и $B(-2; 3)$. Известно, что значение производной в точке $x_{0}$ равно угловому коэффициенту касательной.
\[k=\frac{\Delta y}{\Delta x}=\frac{y_{B}-y_{A}}{x_{B}-x_{A}}=\]
\[\frac{3-4}{-2-(-6)}=-\frac{1}{4}=-0,25\]
\[k=\frac{\Delta y}{\Delta x}=\frac{y_{B}-y_{A}}{x_{B}-x_{A}}=\]
\[\frac{3-4}{-2-(-6)}=-\frac{1}{4}=-0,25\]
Ответ:
-0,25
Задание добавил(а)
Создатель и главный администратор проекта ExamMe.
О задание:
Источник условия: Книга: Математика. Подготовка к ЕГЭ-2017. Профильный уровень. 40 тренировочных вариантов. Под редакцией Ф.Ф. Лысенко, С.Ю. Калабухова.
Источник решения: Книга: Решение заданий из книги указанной в источнике условия. Автор неизвестен.
Источник решения: Книга: Решение заданий из книги указанной в источнике условия. Автор неизвестен.
Обсуждения
Только зарегистрированные пользователи могут оставлять комментарии.
