Найдите площадь поверхности...

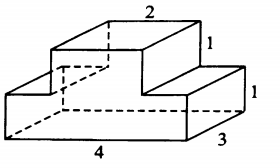
Найдите площадь поверхности многогранника, изображённого на рисунке (все двугранные углы прямые).

Развернём данный многогранник так, чтобы его основанием стала передняя грань (см. рис.). Площадь поверхности $S$ полученного многогранника состоит из площади оснований и площади боковой поверхности. Площадь боковой поверхности равна произведению периметра указанного основания многогранника на его высоту, равную $3$. Осталось заметить, что площадь одного из двух его равных оснований равна сумме площадей двух прямоугольников, имеющих измерения $4 \times 1$ и $1 \times 2$. Отсюда $S=2 \cdot S_{осн.}+S_{бок.}=2 \cdot S_{осн.}+P_{осн.} \cdot h$, где $S_{осн}$, $P_{осн}$ и $h$, соответственно, — площадь основания, периметр основания и высота многогранника. $S = (4 \cdot 1 + 2 \cdot 1) \cdot 2+$ $+ (4 + 1 + 1 + 1 + 2 + 1 + 1 + 1) \cdot 3 = 48.$