ЕГЭ по Математике (профильный)
Основания равнобедренной трапеции...
Задание:
Основания равнобедренной трапеции равны 10 и 90, а её боковые стороны равны 41. Найдите площадь трапеции.
Решение:
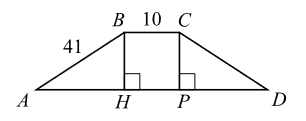
Рассмотрим равнобедренную трапецию $ABCD$, в которой $BC = 10, AD = 90$ - основания, $AB = CD = 41$ (см. рис.). Проведем высоты $CP$ и $BH$. $BCPH$ - прямоугольник, $BC = PH = 10$. Прямоугольные треугольники $ABH$ и $DCP$ равны по гипотенузе и катету ($AB = CD, BH = CP$), тогда $AH = PD = (90 - 10) : 2 = 40$.
Треугольник $ABH$ прямоугольный, $BH=\sqrt{41^{2}-40^{2}}=9$
Площадь трапеции равна $S=\frac{BC+AD}{2}\cdot BH=\frac{10+90}{2}\cdot 9=450$
Треугольник $ABH$ прямоугольный, $BH=\sqrt{41^{2}-40^{2}}=9$
Площадь трапеции равна $S=\frac{BC+AD}{2}\cdot BH=\frac{10+90}{2}\cdot 9=450$
Ответ:
450
Задание добавил(а)
Создатель и главный администратор проекта ExamMe.
О задание:
Источник условия: Книга: Математика. Подготовка к ЕГЭ-2017. Профильный уровень. 40 тренировочных вариантов. Под редакцией Ф.Ф. Лысенко, С.Ю. Калабухова.
Источник решения: Книга: Решение заданий из книги указанной в источнике условия. Автор неизвестен.
Источник решения: Книга: Решение заданий из книги указанной в источнике условия. Автор неизвестен.
Обсуждения
Только зарегистрированные пользователи могут оставлять комментарии.
