ЕГЭ по Математике (профильный)
Окружность, проходящая через вершины...
Задание:
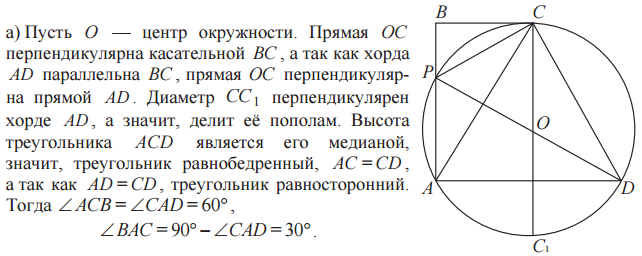
Окружность, проходящая через вершины $A$, $C$ и $D$ прямоугольной трапеции $ABCD$ с основаниями $AD$ и $BC$, пересекает меньшую боковую сторону $AB$ в точке $P$ и касается прямой $BC$. Известно, что $AD = CD$.
а) Докажите, что $CP$ — биссектриса угла $ACB$.
б) В каком отношении прямая $DP$ делит площадь трапеции?
а) Докажите, что $CP$ — биссектриса угла $ACB$.
б) В каком отношении прямая $DP$ делит площадь трапеции?
Решение:

Задание добавил(а)
Создатель и главный администратор проекта ExamMe.
О задание:
Источник условия: Книга: Подготовка к ЕГЭ. Диагностические работы. ЕГЭ 2017. Профильный уровень. Издательство: МЦНМО, 2017
Источник решения: Тот же, что и условия.
Источник решения: Тот же, что и условия.
Обсуждения
Только зарегистрированные пользователи могут оставлять комментарии.
