В правильной четырёхугольной призме...

В правильной четырёхугольной призме $ABCDA_{1}B_{1}C_{1}D_{1}$ сторона основания равна $7$, а боковое ребро - $12$. На рёбрах $A_{1}D_{1}$, $C_{1}D_{1}$ и $CB$ взяты точки $F, K, L$ соответственно так, что $A_{1}F=C_{1}K=CL=3$.

а) Пусть $P$ - точка пересечения плоскости $FKL$ с ребром $AB$. Докажите, что $FKLP$ - прямоугольник.

б) Найдите площадь сечения призмы плоскостью $FKL$

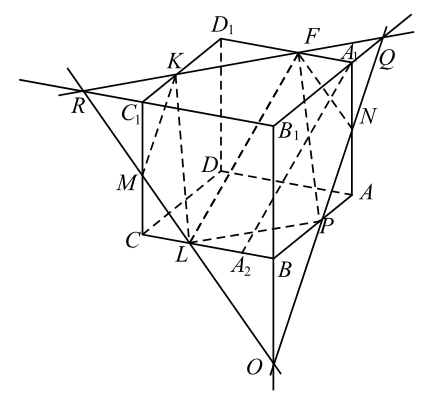
а) Найдём положение точки $P$. Эта точка пересечения плоскости $FKL$ и ребра $AB$, лежащего в плоскости $ABCD$ (см. рис. ). Плоскость $ABCD$ параллельная плоскости $A_{1}B_{1}C_{1}D_{1}$, в которой лежит отрезок $KF$. Плоскость $FKL$ пересекает параллельные плоскости $ABCD$ и $A_{1}B_{1}C_{1}D_{1}$ по параллельным прямым, отсюда $KF \left | \right |LP$. Прямоугольные треугольники $KD_{1}F$ и $LBP$ равны по катету и острому углу $(D_{1}F = LB = 4$ и $\angle D_{1}FK = \angle BLP$ как острые с соответственно параллельными сторонами).

Чтобы доказать, что четырёхугольник $FKLP$ - прямоугольник, найдём длины его сторон и диагонали.

$KF = PL = \sqrt{KD_{1}^{2}+D_{1}F^{2}} = $ $ \sqrt{16+16} = 4\sqrt{2}$
$PF = LK = \sqrt{LC^{2}+CC_{1}^{2}+C_{1}K^{2}} = $ $ \sqrt{9+144+9} = \sqrt{162} = 9\sqrt{2}$
Противоположные стороны четырёхугольника попарно равны, значит, это параллелограмм.

Проведём $A_{1}A_{2}\left | \right | LF$, тогда $LF = A_{1}A_{2} = $ $ \sqrt{(LB-FA_{1})^{2} + AB^{2} + AA_{1}^{2}} = $ $ \sqrt{(BP-C_{1}K)^{2}+CB^{2}+CC_{1}^{2}} = PK$

Диагонали параллелограмма равны, следовательно, $FKLP$ - прямоугольник.

б) Пусть $Q$ и $R$ - точки пересечения прямой $KF$ и прямых $B_{1}C_{1}$ и $A_{1}B_{1}$. Проведём прямые $RL$ и $QP$, они пересекут рёбра $CC_{1}$ и $AA_{1}$ в точках $M$ и $N$ соответственно (см. рис.). Тогда $RC_{1} = KC_{1} = CL$, поэтому можно доказать, что равны треугольники $RC_{1}M$ и $MCL$. Прямая $RL$, а значит, и плоскость $FKL$ пересекают ребро $CC_{1}$ в его середине - точке $M$. Аналогично плоскость $FKL$ пересекает ребро $AA_{1}$ в его середине - точке $N$.

В диагональном сечении $CC_{1}A_{1}A$, которое является прямоугольником, отрезок $MN$ - средняя линия. В прямоугольнике $MCAN$ противоположные стороны равны: $MN = CA = 7 \sqrt{2}$.

Сечение $FKMLPN$ состоит из двух равных трапеций $MKFN$ и $MLPN$, причём мы доказали, что $LK \perp KF$ и $LK \perp LP$. Высота каждой из этих трапеций равна $\frac{LK}{2} = \frac{9\sqrt{2}}{2}$.

$S_{сечения} = $ $ 2S_{MKFN} = $ $ 2\cdot \frac{KF+MN}{2}\cdot \frac{LK}{2} = $ $ (4\sqrt{2}+7\sqrt{2})\cdot \frac{9\sqrt{2}}{2} = 99 $

Ответ: $99$