Решите неравенство \[\left ( 7x-10...

Решите неравенство \[\left ( 7x-10 \right )log_{4x-3}(x^{2}-4x+9)\geq 0\]

В правой части неравенства стоит $0$, в левой - произведение двух множителей. Определим знаки каждого из этих множителей.

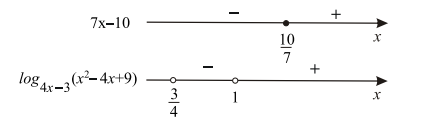
При $x=\frac{10}{7}$ выражение $7x-10=0$, при $x > \frac{10}{7}$ выражение $7x-10>0$, а при $x< \frac{10}{7}$ выражение $7x-10<0$.

Рассмотрим выражение $log_{4x-3}(x^2-4x+9)$. Заметим, что $x^{2}-4x+9 = $ $ (x-2)^{2}+5\geq 5$ при любых значениях $x$. Значит, при $4x-3>1$, то есть при $x>1$, выражение $log_{4x-3}(x^2-4x+9) > 0 $; при $0 < 4x-3 < 1$, то есть при $\frac{3}{4} < x < 1$, $log_{4x-3}(x^2-4x+9) < 0 $ и не определено при $x\leq \frac{3}{4}$ и $x=1$.

Удобно знаки сомножителей отметить на двух параллельных прямых (см. рис.)

Таким образом, решение исходного неравенства: $ \frac{3}{4} < x < 1 ; x \geq \frac{10}{7} $.

Ответ: $\left ( \frac{3}{4};1\right );[\frac{10}{7};+\infty)$