ЕГЭ по Математике (профильный)
Один острый угол прямоугольного...
Задание:
Один острый угол прямоугольного треугольника на $74^{\circ}$ больше другого. Найдите больший острый угол. Ответ дайте в градусах.
Решение:
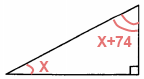
Пусть один острый угол будет равен $x$, а второй острый угол $x+74$, тогда, зная что сумма углов треугольника равна $180^{\circ}$, можно записать уравнение:
$x+(x+74^{\circ})+90^{\circ}=180^{\circ}$.
$2x = 180^{\circ} - 90^{\circ} - 74^{\circ} $
$2x = 16^{\circ}$
$x = \frac{16^{\circ}}{2} = 8^{\circ}$
Больший острый угол равен $8^{\circ}+74^{\circ} = 82^{\circ}$
$x+(x+74^{\circ})+90^{\circ}=180^{\circ}$.
$2x = 180^{\circ} - 90^{\circ} - 74^{\circ} $
$2x = 16^{\circ}$
$x = \frac{16^{\circ}}{2} = 8^{\circ}$
Больший острый угол равен $8^{\circ}+74^{\circ} = 82^{\circ}$
Ответ:
82
Задание добавил(а)
Создатель и главный администратор проекта ExamMe.
О задание:
Источник условия: Банк зада ФИПИ (fipi.ru)
Источник решения: Авторский коллектив проекта ExamMe.RU
Источник решения: Авторский коллектив проекта ExamMe.RU
Обсуждения
Только зарегистрированные пользователи могут оставлять комментарии.
