ЕГЭ по Математике (профильный)
В треугольнике $ABC$ стороны $AC$ и...
Задание:
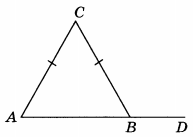
В треугольнике $ABC$ стороны $AC$ и $BC$ равны. Внешний угол при вершине $B$ равен $110^{\circ}$. Найдите угол $C$. Ответ дайте в градусах.
Решение:
Углы $CBD$ и $ABC$ смежные, значит $\angle ABC = 180^{\circ} - 110^{\circ} = 70^{\circ}$.
$\angle ABC = \angle CAB = 70^{\circ}$, так как треугольник $ABC$ - равнобедренный $(AC = BC)$.
$\angle C^{\circ} = 180^{\circ} - 70^{\circ} - 70^{\circ} = 40^{\circ}$
$\angle ABC = \angle CAB = 70^{\circ}$, так как треугольник $ABC$ - равнобедренный $(AC = BC)$.
$\angle C^{\circ} = 180^{\circ} - 70^{\circ} - 70^{\circ} = 40^{\circ}$
Ответ:
40
Задание добавил(а)
Создатель и главный администратор проекта ExamMe.
О задание:
Источник условия: Банк зада ФИПИ (fipi.ru)
Источник решения: Авторский коллектив проекта ExamMe.RU
Источник решения: Авторский коллектив проекта ExamMe.RU
Обсуждения
Только зарегистрированные пользователи могут оставлять комментарии.
