ЕГЭ по Математике (профильный)
Центральный угол на $33^{\circ}$...
Задание:
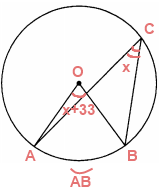
Центральный угол на $33^{\circ}$ больше острого вписанного угла, опирающегося на ту же дугу окружности. Найдите вписанный угол. Ответ дайте в градусах.
Решение:
Пусть величина вписанного угла равна $x$, тогда величина центрального угла равна $x+33^{\circ}$. Зная, что величина центрального угла равна величине дуги на которую она опирается, а величина вписанного угла равна половине дуги на которую она опирается, можно составить следующее уравнение.
$\angle C = \frac{\angle O}{2}$
$x = \frac{x+33^{\circ}}{2}$
$2x = x + 33^{\circ}$
$2x - x = 33^{\circ}$
$x = 33^{\circ}$
$\angle C = \frac{\angle O}{2}$
$x = \frac{x+33^{\circ}}{2}$
$2x = x + 33^{\circ}$
$2x - x = 33^{\circ}$
$x = 33^{\circ}$
Ответ:
33
Задание добавил(а)
Создатель и главный администратор проекта ExamMe.
О задание:
Источник условия: Банк зада ФИПИ (fipi.ru)
Источник решения: Авторский коллектив проекта ExamMe.RU
Источник решения: Авторский коллектив проекта ExamMe.RU
Обсуждения
Только зарегистрированные пользователи могут оставлять комментарии.
