ЕГЭ по Математике (профильный)
Точка $E$ - середина боковой стороны...
Задание:
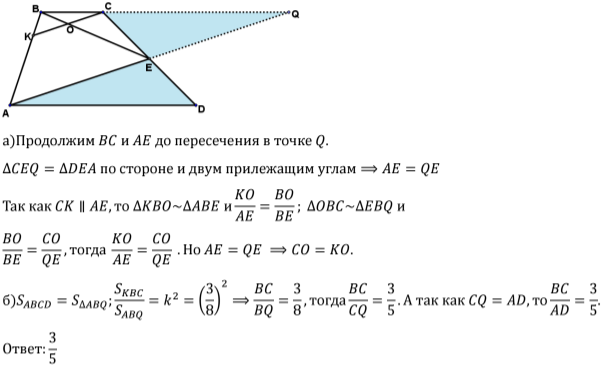
Точка $E$ - середина боковой стороны $CD$ трапеции $ABCD$. На её стороне $AB$ взяли точку $K$ так, что прямые $CK$ и $AE$ параллельны. Отрезки $CK$ и $BE$ пересекаются в точке $O$.
а) Докажите, что $CO=KO$.
б) Найдите отношение оснований трапеции $BC:AD$, если площадь треугольника $BCK$ составляет $\frac{9}{64}$ площади всей трапеции $ABCD$.
а) Докажите, что $CO=KO$.
б) Найдите отношение оснований трапеции $BC:AD$, если площадь треугольника $BCK$ составляет $\frac{9}{64}$ площади всей трапеции $ABCD$.
Решение:
Задание добавил(а)
Создатель и главный администратор проекта ExamMe.
О задание:
Источник условия: ЕГЭ 2017, основная волна (2 июня)
Источник решения: Форум alexlarin.net
Источник решения: Форум alexlarin.net
Обсуждения
Только зарегистрированные пользователи могут оставлять комментарии.
