ЕГЭ по Математике (профильный)
В треугольнике $ABC$ угол $A$ равен...
Задание:
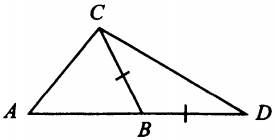
В треугольнике $ABC$ угол $A$ равен $65^{\circ}$, угол $C$ равен $53^{\circ}$. На продолжении стороны $AB$ за точку $B$ отложен отрезок $BD$, равный стороне $BC$ (см. рис.). Найдите угол $D$ треугольника $BCD$. Ответ дайте в градусах.
Решение:
Угол $CBD$ является внешним углом треугольника $ABC$ и равен сумме двух углов треугольника, не смежных с ним. Найдём угол $CBD$.
$\angle CBD$ $=$ $\angle A + \angle C$ $=$ $65^{\circ} + 53^{\circ} $=$ 118^{\circ}$. Треугольник $BCD$ равнобедренный, его углы при основании равны: $\angle D = \angle DCB$. Сумма углов треугольника равна $180^{\circ}$. Тогда $\angle D = (180^{\circ} - 118^{\circ}):2 = 31^{\circ}$.
$\angle CBD$ $=$ $\angle A + \angle C$ $=$ $65^{\circ} + 53^{\circ} $=$ 118^{\circ}$. Треугольник $BCD$ равнобедренный, его углы при основании равны: $\angle D = \angle DCB$. Сумма углов треугольника равна $180^{\circ}$. Тогда $\angle D = (180^{\circ} - 118^{\circ}):2 = 31^{\circ}$.
Ответ:
31
Задание добавил(а)
Создатель и главный администратор проекта ExamMe.
О задание:
Источник условия: Книга: Математика. Подготовка к ЕГЭ-2017. Профильный уровень. 40 тренировочных вариантов. Под редакцией Ф.Ф. Лысенко, С.Ю. Калабухова.
Источник решения: Книга: Решение заданий из книги указанной в источнике условия. Автор неизвестен.
Источник решения: Книга: Решение заданий из книги указанной в источнике условия. Автор неизвестен.
Обсуждения
Только зарегистрированные пользователи могут оставлять комментарии.

Создатель и главный администратор проекта ExamMe.