В основании прямой призмы лежит...

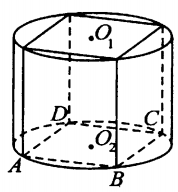
В основании прямой призмы лежит квадрат со стороной $6$. Боковое ребро призмы равно $\frac{6}{\pi}$. Найдите объём цилиндра, описанного около этой призмы (см. рис.)

Рассмотрим рисунок, указанный в условии. Диаметр основания цилиндра является диагональю $AC$ квадрата $ABCD$, а радиус $R$ основания цилиндра равен половине $AC$. Согласно теореме Пифагора $AC=\sqrt{AB^{2}+BC^{2}}$ $=\sqrt{6^{2}+6^{2}}$ $=\sqrt{72} = 6\cdot \sqrt{2}$.

$R=3\cdot \sqrt{2}$. Заметим, что высота цилиндра совпадает с высотой призмы $h$. Отсюда следует, что $V_{цил.} = S_{осн.}\cdot h$ $=\pi \cdot R^{2} \cdot h$ $= \pi \cdot (3\sqrt{2})^{2}\cdot \frac{6}{\pi}$ $= 18\cdot 6 = 108$.