ЕГЭ по Математике (профильный)
Найдите точку минимума функции...
Задание:
Найдите точку минимума функции $y=2x^{3} + 36x^{2} + 162x + 57$.
Решение:
Найдём производную исходной функции: $y'(x) = 6x^{2}+72x+162$.
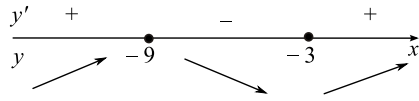
Найдём нули производной из уравнения $y'(x) = 0$; $6x^{2} + 72x + 162 = 0$; $ $ $x^{2}+12x+27=0$, $x_{1,2} = -6\pm \sqrt{6^{2}-1\cdot 27}$ $=-6\pm 3$. Отсюда $x_{1} = -9$, $x_{2}=-3$. Расставим знаки производной и определим промежутки монотонности исходной функции (см. рис.). Из рисунка видно, что значение $x = -3$ является единственной точкой минимума.
Найдём нули производной из уравнения $y'(x) = 0$; $6x^{2} + 72x + 162 = 0$; $ $ $x^{2}+12x+27=0$, $x_{1,2} = -6\pm \sqrt{6^{2}-1\cdot 27}$ $=-6\pm 3$. Отсюда $x_{1} = -9$, $x_{2}=-3$. Расставим знаки производной и определим промежутки монотонности исходной функции (см. рис.). Из рисунка видно, что значение $x = -3$ является единственной точкой минимума.
Ответ:
-3
Задание добавил(а)
Создатель и главный администратор проекта ExamMe.
О задание:
Источник условия: Книга: Математика. Подготовка к ЕГЭ-2017. Профильный уровень. 40 тренировочных вариантов. Под редакцией Ф.Ф. Лысенко, С.Ю. Калабухова.
Источник решения: Книга: Решение заданий из книги указанной в источнике условия. Автор неизвестен.
Источник решения: Книга: Решение заданий из книги указанной в источнике условия. Автор неизвестен.
Обсуждения
Только зарегистрированные пользователи могут оставлять комментарии.
