а) Решите уравнение...

а) Решите уравнение $6log^{2}_{2}(2cosx)-9log_{2}(2cosx)+3=0$.
б) Найдите все корни этого уравнения, принадлежащие отрезку $[-\frac{\pi}{2};\pi]$.

Решим уравнение $6log^{2}_{2}(2cosx)-9log_{2}(2cosx)+3=0$. Обозначим $log_{2}(2cosx)=t$ и решим получившееся квадратное уравнение.


$6t^{2}-9t+3=0, t=\frac{9\pm3}{12}$; $t_{1}=\frac{1}{2}$; $t_{2}=1$.

$\left[
\begin{gathered}
\log_{2}(2cosx)=\frac{1}{2},\\
\log_{2}(2cosx)=1; \\
\end{gathered}
\right.$

$\left[
\begin{gathered}
2cosx=\sqrt{2},\\2cosx=2;\\
\end{gathered}
\right.$

$\left[
\begin{gathered}
cosx = \frac{\sqrt{2}}{2},\\cosx = 1;\\
\end{gathered}
\right.$

$\left[ \begin{gathered}x=\pm \frac{\pi}{4}+2\pi n, n \in Z\\x = 2\pi k, k \in Z.\\ \end{gathered}
\right.$

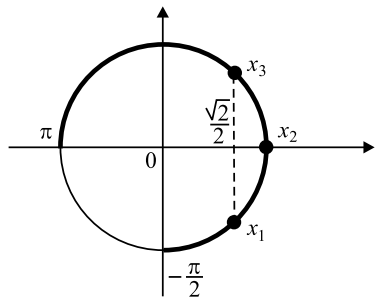
б) Корни, принадлежащие отрезку $[-\frac{\pi}{2};\pi]$, найдём с помощью числовой окружности: $x_{1}= -\frac{\pi}{4}$; $x_{2}=0$; $x_{3}=\frac{\pi}{4}$ (см. рис)

$Ответ:$ а)$\pm\frac{\pi}{4} + 2\pi n$, $n \in Z$; $2\pi k, k \in Z$; б) $-\frac{\pi}{4}$; $0$; $\frac{\pi}{4}$.