В трапеции $ABCD$, в которой $AD...

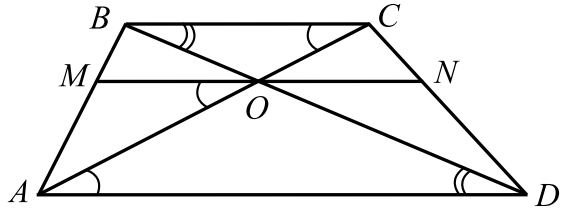
В трапеции $ABCD$, в которой $AD \parallel BC$, точка $O$ - точка пересечения диагоналей трапеции. Через эту точку проведена прямая, параллельная основаниям и пересекающая боковые стороны в точках $M$ и $N$.

а) Докажите, что $MO=ON$

б) Найдите отношение $\frac{BC}{AD}$, если $\frac{BD}{OB}=\frac{5}{2}$.

а) 1. $\triangle AOD \sim \triangle BOC$ (по двум углам: $\angle BCO = \angle CAD$ как накрест лежащие при параллельных прямых $AD$ и $BC$ и секущей $AC$, $\angle CBO = \angle ODA$ как накрест лежащие при параллельных прямых $AD$ и $BC$ и секущей $BD$) (см. рис.).

Отсюда следует, что $\frac{BO}{OD} = \frac{OC}{AO}$. Тогда $\frac{BO}{OD} + 1 = \frac{OC}{AO} + 1$, $\frac{BO+OD}{OD} = \frac{OC+AO}{AO}$, $\frac{BD}{OD} = \frac{AC}{AO}$. $(1)$

2. $\triangle ABC \sim \triangle AMO$ (по двум углам: $\angle BCA = \angle MOA$, $\angle BAC$ - общий). Следовательно, $\frac{BD}{OD} = \frac{AC}{AO}$. $(1)$

Аналогично $\triangle DBC \sim \triangle DON$ $\Rightarrow \frac{BC}{ON} = \frac{BD}{OD}$. С учётом $(1)$, получим: $\frac{BC}{ON} = \frac{AC}{AO}$. Из этого равенства, с учётом (2), получим: $\frac{BC}{ON} = \frac{BC}{MO}$. Следовательно, $ON = MO$.

б) $\frac{BC}{AD} = \frac{BO}{OD}$ $= \frac{BO}{BD-BO}$,

$\frac{AD}{BC}=\frac{BD-BO}{BO}$ $=\frac{BD}{BO} - 1 = \frac{5}{2} - 1 = \frac{3}{2}$. Тогда $\frac{BC}{AD} = \frac{2}{3}$.

$Ответ:$ $\frac{2}{3}$.