ЕГЭ по Математике (профильный)
На рисунке изображены график функции...
Задание:
На рисунке изображены график функции $y = f(x)$ и касательная к нему в точке с абсциссой $x_0$. Найдите значение производной функции $f(x)$ в точке $x_0$.
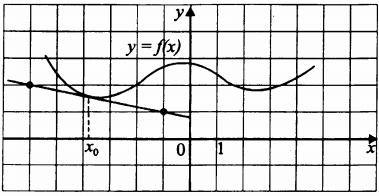
Решение:
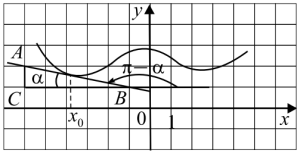
По рисунку определяем, что касательная проходит через точки $A(-6; 2)$ и $B(?1; 1)$. Обозначим через $C(-6; 1)$ точку пересечения прямых $x = -6$ и $y = 1$, а через $\alpha$ угол $ABC$ (на рисунке видно, что он острый). Тогда прямая $AB$ образует с положительным направлением оси $Ox$ угол $\pi - \alpha$, который является тупым.
Как известно, $tg(\pi - \alpha)$ и будет значением производной функции f(x) в точке $x_0$.
Заметим, что $tg \alpha = \frac{AC}{CB} =$ $\frac{2-1}{-1-(-6)} = \frac{1}{5}$. Отсюда по формулам приведения получаем:
$tg(\pi - \alpha) = - tg \alpha$ $= -\frac{1}{5} = -0,2$
Как известно, $tg(\pi - \alpha)$ и будет значением производной функции f(x) в точке $x_0$.
Заметим, что $tg \alpha = \frac{AC}{CB} =$ $\frac{2-1}{-1-(-6)} = \frac{1}{5}$. Отсюда по формулам приведения получаем:
$tg(\pi - \alpha) = - tg \alpha$ $= -\frac{1}{5} = -0,2$
Ответ:
-0,2
Задание добавил(а)
Создатель и главный администратор проекта ExamMe.
О задание:
Источник условия: Книга: Математика. Подготовка к ЕГЭ-2017. Профильный уровень. 40 тренировочных вариантов. Под редакцией Ф.Ф. Лысенко, С.Ю. Калабухова.
Источник решения: Тот же, что и условия
Источник решения: Тот же, что и условия
Обсуждения
Только зарегистрированные пользователи могут оставлять комментарии.
