На рисунке изображён график функции...

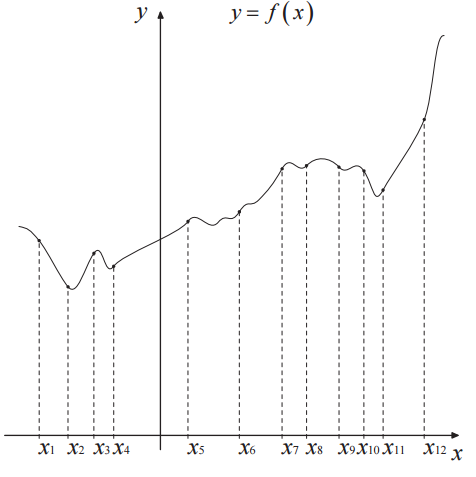
На рисунке изображён график функции y = f(x) и двенадцать точек на оси абсцисс: $x_{1}, x_{2}, x_{3}, x_{4}, x_{5}, x_{6}, x_{7}, x_{8}, x_{9}, x_{10}, x_{11}, x_{12}$. В скольких из этих точек производная функции f(x) положительна?

Для решения этого задания необходимо знать геометрический смысл производной, который формулируется так: Производная в точке $x_{0}$ равна угловому коэффициенту касательной (значение тангенса угла между касательной и осью абсцисс - ось Ox) к графику функции y = f(x) в этой точке.

На мой взгляд определение далеко не из простых. Поэтому, чтобы в нем разобраться давайте применим это к нашему рисунку.

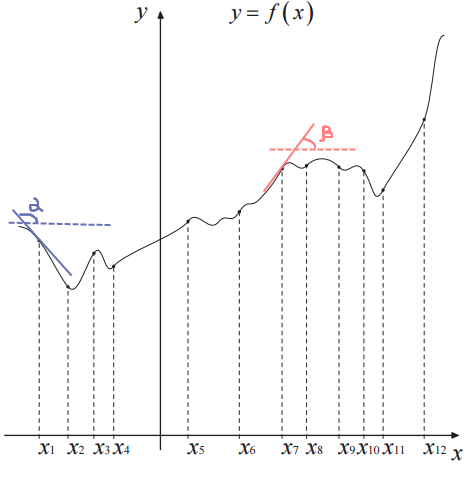
Рассмотрим на примере точки $x_{1}$ и $x_{7}$. Проведем касательные к этим точкам фиолетовая и розовая. Как мы видим по рисунку угол $\alpha$ - тупой, а значит значение тангенса этого угла отрицательное, следовательно и производная функции в этой точке отрицательная. Угол $\beta$ - острый, следовательно значение тангенса этого положительное положительное, как и производная.

То есть из этих сложных теоретических выкладок просматривается элементарная аналогия. Если функция убывает, значит производная функции в этой точке отрицательна, если возрастает - положительна.

Отвечаем на наш вопрос - производная функции положительная в точках $x_{3}, x_{4}, x_{5}, x_{6}, x_{7}, x_{8}, x_{11}, x_{12}$. Ответ: 8 точек.