В правильной четырёхугольной призме...

В правильной четырёхугольной призме $ABCDA_{1}B_{1}C_{1}D_{1}$ сторона основания $AB=4\sqrt{2}$, боковое ребро $AA_{1}=8$, $M$ середина ребра $A_{1}B_{1}$.

На ребре $DD_{1}$ отмечена точка $L$ так,что $DL=2$. Плоскость $\gamma$ параллельна прямой $A_{1}C_{1}$ и содержит точки $M$ и $A$.

а) Докажите, что прямая $BL$ перпендикулярна плоскости $\gamma$.

б) Найдите объём пирамиды, вершина которой точка $B$, а основание - сечение данной пирамиды плоскостью $\gamma$.

а) Построим сечение призмы плоскостью $\gamma$ (см. рис.1)

Плоскость $\gamma$ пересекает плоскость $ABC$ по прямой $AC$, а плоскость $A_{1}B_{1}C_{1}$ — по прямой $MN$ ($N$ — середина $B_{1}C_{1}$), проходящей через точку $M$, параллельной $A_{1}C_{1}$ (если плоскость проходит через прямую, параллельную другой плоскости, и пересекает её, то линия пересечения параллельна это прямой). $AMNC$ — сечение пирамиды плоскостью $\gamma$. $AMNC$ — равнобедренная трапеция (см. рис.2). $AMNC || A_{1}C_{1}$.

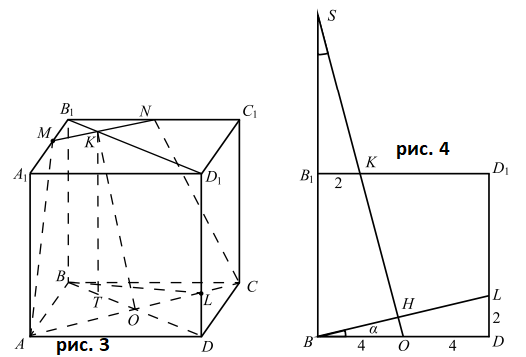
Рассмотрим диагональное сечение $BB_{1}D_{1}D$ призмы $ABCDA_{1}B_{1}C_{1}D_{1}$ (см. рис.3). $BB_{1}D_{1}D$ — квадрат, так как $BB_{1} = BD = 8$. $O$ — точка пересечения диагоналей $AC$ и $BD$ квадрата $ABCD$ со стороной, равной $4\sqrt{2}$, значит, $AO = OC = 4$.
$MN$ — средняя линия треугольника $A_{1}B_{1}C_{1}$, $MK = KN$, $B_{1}K=\frac{1}{4}B_{1}D_{1}=2$.
Пусть $\angle DBL = \alpha$ (см. рис.4), тогда в прямоугольном треугольнике $DBL$ $\angle BLD = 90^{\circ} — \alpha$. $\triangle SBO \sim \triangle B_{1}SK$ с коэффициентом подобия $2$, следовательно, $SB_{1} = 8$. $\triangle B_{1}SK$ $= \triangle DBL$ по двум катетам. Значит, $\triangle BSO = \alpha$, $\triangle BOS = 90^{\circ} — \alpha$, $\angle HOD = 180^{\circ} - \angle HOB$ $= 180 - (90^{\circ} - \alpha)$ $= 90^{\circ} + \alpha$. В выпуклом четырёхугольнике $OHLD$ сумма углов равна $360^{\circ} : \angle O + \angle H$ $+ \angle L + \angle D = 360^{\circ}$, $\angle H = 360^{\circ} - (90^{\circ} + \alpha)$ $- (90^{\circ} - a) -$ $90^{\circ} = 90^{\circ}$.

Итак, доказано, что $BL\perp KO$, кроме того, $AC$ перпендикулярна плоскости $BB_{1}D_{1}$,а значит, $AC$ перпендикулярна любой прямой этой плоскости, в частности прямой $BL$. Прямая $BL$ перпендикулярна двум пересекающимся прямым плоскости $\gamma$, следовательно, $BL \perp \gamma$. Что и требовалось доказать.

б) $V_{BAMNC} = \frac{1}{3}S_{AMNC}\cdot BH=$ $\frac{1}{3} \cdot \frac{MN+AC}{2} \cdot KO \cdot BH$.

$MN = 4$, $AC=8$, $KO$ найдём по теореме Пифагора как гипотенузу прямоугольного треугольника $KOT$, где $KT \parallel BB_{1}$ (см. рис.3), с катетами $KT = 8$ и $OT = TB = 2$.

$KO = \sqrt{KT^{2}+OT^{2}}=$ $\sqrt{8^{2}+2^{2}}=$ $=2\sqrt{17}$.

Рассмотрим рисунок 4. $BH$ найдём из подобия прямоугольных треугольников $BHO$ и $SBO$ ($\angle HBO = \angle BSO$): $\frac{BH}{BO} = \frac{SB}{SO}$. $BO = 4$, $SB =16$. Из подобия треугольников $SBO$ и $B_{1}SK$ с коэффициентом подобия $2$ следует, что $SO = 2KO = 4\sqrt{17}$.

$\frac{BH}{4} = \frac{16}{4\sqrt{17}}$, $BH = \frac{16}{\sqrt{17}}$. $V_{BAMNC}=\frac{1}{3}\cdot \frac{MN+AC}{2}\cdot KO \cdot BH$ $=\frac{1}{3}\cdot \frac{4+8}{2}\cdot 2\sqrt{17} \cdot \frac{16}{\sqrt{17}} = 64$.

$Ответ:$ $64$.