ЕГЭ по Математике (профильный)
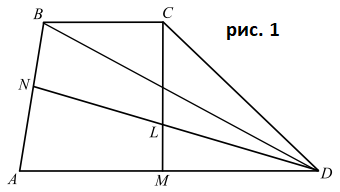
В трапеции $ABCD$ точка $M$ —...
Задание:
В трапеции $ABCD$ точка $M$ — середина основания $AD$, точка $N$ выбрана на стороне $AB$ так, что площадь четырёхугольника $ANLM$ равна площади треугольника $CLD$, где $L$ — точка пересечения отрезков $CM$ и $DN$.
а) Докажите, что $N$ — середина стороны $AB$.
б) Найдите, какую часть от площади трапеции $ABCD$ составляет площадь четырёхугольника $ANLM$, если $BC = 5$, $AD = 8$.
а) Докажите, что $N$ — середина стороны $AB$.
б) Найдите, какую часть от площади трапеции $ABCD$ составляет площадь четырёхугольника $ANLM$, если $BC = 5$, $AD = 8$.
Решение:
а) По условию $S_{ANLM} = S_{CLD}$ (см. рис.1), следовательно, $S_{ANLM}+S_{LMD}$ $= S_{CLD}+S_{LMD}$, $S_{ANLM}+S_{LMD}$ $=$ $S_{AND}$, $S_{CLD}+S_{LMD}$ $=$ $S_{CMD}$, значит, $S_{AND} = S_{CMD}\cdot 2S_{AND} =$ $2S_{CMD} = S_{ACD} = S_{ABD}$ (треугольники $ACD$ и $ABD$ имеют общее основание $AD$ и общую высоту). Итак, $2S_{AND} = S_{ABD} = S_{AND} + S_{BND}$, откуда следует, что $S_{AND} = S_{BND}$, а это означает, что точка $N$ — середина стороны $AB$ (у треугольников $AND$ и $BND$ общая высота).
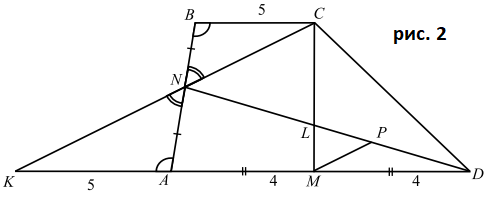
б) Пусть $K$ — точка пересечения прямых $CN$ и $AD$ (см. рис.2). Заметим, что $S_{ABCD} = S_{CKD}$ ($\triangle AKN = \triangle BCN$ по второму признаку равенства треугольников) и $\frac{CL}{CM} = \frac{S_{CLD}}{S_{CMD}}$.
Проведём $MP\parallel KC$, тогда из подобия треугольников $NCL$ и $LMP$ ($\angle MLP = \angle NLC$, $\angle LPM = \angle CNL$) $\frac{CL}{LM} = \frac{CN}{MP}=$ $\frac{KN}{MP}$.
Из подобия треугольников $KND$ и $DMP$ ($KN\parallel MP$)
$\frac{KN}{MP} = \frac{KD}{MD} =$ $ \frac{13}{4}$. Значит, $\frac{CL}{LM} = \frac{KN}{MP}=$ $\frac{13}{4}$; $4CL = 13CM-13CL$, $17CL = 13CM$, следовательно, $\frac{CL}{LM} = \frac{13}{17}=$ $\frac{S_{CLD}}{S_{CMD}}$, откуда $S_{CLD} = \frac{13}{17}S_{CMD}$.
$\frac{S_{CMD}}{S_{CKD}}$ $=$ $\frac{MD}{KD}= \frac{4}{13}$, откуда $S_{CMD} = \frac{4}{13}S_{CKD} = \frac{4}{13}S_{ABCD}$.
Подставляя $S_{CMD} = \frac{4}{13}$ $ $ $ S_{ABCD}$ в равенство $S_{CLD} = \frac{13}{17}$ $ $ $S_{CMD}$, получим $S_{CLD} = \frac{13}{17}\cdot S_{CMD}=$ $\frac{13}{17} \cdot \frac{4}{13}$ $ $ $S_{ABCD} = \frac{4}{17} S_{ABCD}$. Учитывая, что $S_{ANLM} = S_{CLD}$, окончательно получим: $S_{ANLM} = \frac{4}{17} S_{ABCD}$.
$Ответ:$ $\frac{4}{17}$
б) Пусть $K$ — точка пересечения прямых $CN$ и $AD$ (см. рис.2). Заметим, что $S_{ABCD} = S_{CKD}$ ($\triangle AKN = \triangle BCN$ по второму признаку равенства треугольников) и $\frac{CL}{CM} = \frac{S_{CLD}}{S_{CMD}}$.
Проведём $MP\parallel KC$, тогда из подобия треугольников $NCL$ и $LMP$ ($\angle MLP = \angle NLC$, $\angle LPM = \angle CNL$) $\frac{CL}{LM} = \frac{CN}{MP}=$ $\frac{KN}{MP}$.
Из подобия треугольников $KND$ и $DMP$ ($KN\parallel MP$)
$\frac{KN}{MP} = \frac{KD}{MD} =$ $ \frac{13}{4}$. Значит, $\frac{CL}{LM} = \frac{KN}{MP}=$ $\frac{13}{4}$; $4CL = 13CM-13CL$, $17CL = 13CM$, следовательно, $\frac{CL}{LM} = \frac{13}{17}=$ $\frac{S_{CLD}}{S_{CMD}}$, откуда $S_{CLD} = \frac{13}{17}S_{CMD}$.
$\frac{S_{CMD}}{S_{CKD}}$ $=$ $\frac{MD}{KD}= \frac{4}{13}$, откуда $S_{CMD} = \frac{4}{13}S_{CKD} = \frac{4}{13}S_{ABCD}$.
Подставляя $S_{CMD} = \frac{4}{13}$ $ $ $ S_{ABCD}$ в равенство $S_{CLD} = \frac{13}{17}$ $ $ $S_{CMD}$, получим $S_{CLD} = \frac{13}{17}\cdot S_{CMD}=$ $\frac{13}{17} \cdot \frac{4}{13}$ $ $ $S_{ABCD} = \frac{4}{17} S_{ABCD}$. Учитывая, что $S_{ANLM} = S_{CLD}$, окончательно получим: $S_{ANLM} = \frac{4}{17} S_{ABCD}$.
$Ответ:$ $\frac{4}{17}$
Задание добавил(а)
Создатель и главный администратор проекта ExamMe.
О задание:
Источник условия: Книга: Математика. Подготовка к ЕГЭ-2017. Профильный уровень. 40 тренировочных вариантов. Под редакцией Ф.Ф. Лысенко, С.Ю. Калабухова.
Источник решения: Книга: Решение заданий из книги указанной в источнике условия. Автор неизвестен.
Источник решения: Книга: Решение заданий из книги указанной в источнике условия. Автор неизвестен.
Обсуждения
Только зарегистрированные пользователи могут оставлять комментарии.
