Найдите все значения $a$, при каждом...

Найдите все значения $a$, при каждом из которых уравнение $\frac{3x+a-x^{2}+4a^{2}x-x^{3}}{4a^{2}x-x^{3}}=1$ имеет единственный корень.

В левой части уравнения выделим целую часть

$\frac{3x+a-x^{2}+4a^{2}x-x^{3}}{4a^{2}x-x^{3}}=$ $\frac{4a^{2}x-x^{3}}{4a^{2}x-x^{3}}+$ $\frac{-x^{2}+3x+a}{4a^{2}x-x^{3}}=$ $1+\frac{-x^{2}+3x+a}{4a^{2}x-x^{3}}$.

Тогда уравнение примет вид $\frac{-x^{2}+3x+a}{4a^{2}x-x^{3}}=0$. Оно равносильно системе

$\small \begin{cases} -x^{2}+3x+a=0, \\ 4a^{2}x-x^{3}\neq 0; \end{cases}$ $\small \begin{cases} a=x^{2}-3x, \\ x\neq 0, x \neq \pm 2a. \end{cases}$

Решим систему графически в системе координат $xOa$. Для этого строим графики функций $a=x^{2}-3x$ и $a=\pm \frac{x}{2}$.

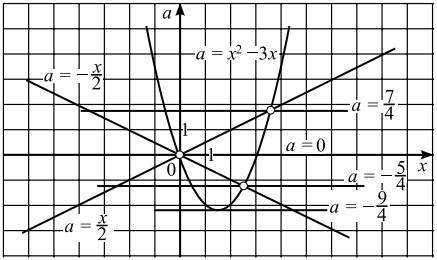
Графиком функции $a=x^{2}-3x$ является парабола, ветви которой направлены вверх. Вершина параболы — точка $(\frac{3}{2};-\frac{9}{4})$. точки $(0;0)$ и $(3; 0)$ принадлежат параболе. Графиками функций $a = \pm \frac{x}{2}$ являются прямые.

Решая уравнение $x^{2}-3x=\frac{x}{2}$, находим точки пересечения прямой $a=\frac{x}{2}$ и параболы $a=x^{2}-3x;$ $x=0$, $x=\frac{7}{2}$, откуда $a = 0$, $а =\frac{7}{4}$. Аналогично, решая уравнение $x^{2}-3x=-\frac{x}{2}$ находим $x = 0$, $x=\frac{5}{2}$. Тогда $a = 0$, $a =-\frac{5}{4}$. Выкалываем эти точки (см. рис.).

По рисунку видим, что ровно одна точка пересечения параболы с каждой из прямых при $a=-\frac{9}{4}$, $a=-\frac{5}{4}$, $a=0$, $a=\frac{7}{4}$.

$Ответ:$ $-\frac{9}{4}$; $-\frac{5}{4}$; $0$; $\frac{7}{4}$.