В цилиндрическом сосуде уровень...

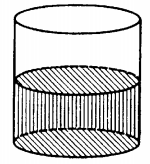
В цилиндрическом сосуде уровень жидкости достигает $20$ см (см. рис.). На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в два раза больше диаметра первого? Ответ выразите в сантиметрах.

Пусть $R$ — радиус основания первого сосуда, тогда $2R$ — радиус основания второго сосуда. По условию объём жидкости $V$ в первом и втором сосуде один и тот же. Обозначим через $H$ — уровень, на который поднялась жидкость во втором сосуде. Тогда $V=\pi R^{2}\cdot 20$, и $V=\pi(2R)^{2}H= 4\pi R^{2}H$. Отсюда $\pi R^{2}\cdot 20 = 4\pi R^{2}H$, $20 = 4H$, $H=5$.