Окружность, вписанная в...

Окружность, вписанная в остроугольный треугольник $ABC$, касается сторон $BA$ и $BC$ в точках $M$ и $N$.

а) Докажите, что центр окружности, вписанной в треугольник $BMN$, лежит на окружности, вписанной в треугольник $ABC$.

б) Найдите расстояние между центрами этих окружностей, если $AB = 10$, $AC = 12$, $sinA = \frac{\sqrt{7}}{4}$.

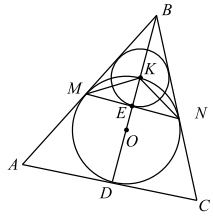
а) Пусть точка $O$ — центр окружности, вписанной в $\triangle ABC$ (см. рис.).

Биссектриса $BD$ пересекает дугу $MN$ в точке $K$, а отрезок $MN$ в точке $E$. $BM = MN$ как отрезки касательных, проведённых к окружности из одной точки, отсюда $\triangle MBN$ — равнобедренный, значит, биссектриса $BE$ — медиана и высота. $\triangle KME = \triangle KNE$ по двум катетам ($ME = NE$, $KE$ — общая сторона). Из равенства треугольников следует: $MK = NK$, а так как равные хорды стягивают равные дуги, то $\smile KM = \smile KN$.

Докажем, что $K$ — центр вписанной окружности треугольника $\triangle MBN$.

$\angle KMN = \frac{1}{2} \smile NK$ как вписанный, $\angle KMB = \frac{1}{2}\smile MK$ как угол между касательной $BM$ и хордой $KM$. $\smile MK = \smile NK$, значит, $ \angle KMN = \angle KMB$, тогда $MK$ — биссектриса угла $NMB$.

Отсюда следует, что $K$ — точка пересечения $BE$ и $MK$, то есть точка пересечения биссектрис $\triangle BMN$, а значит, центр вписанной окружности.

б) По доказанному в пункте а) центр вписанной окружности $\triangle BMN$ лежит на вписанной окружности $\triangle ABC$, следовательно, искомое расстояние равно радиусу вписанной окружности $\triangle ABC$.

Из формулы $S_{ABC} = p\cdot r$ следует, что $r=\frac{S_{ABC}}{p}$ -радиус вписанной окружности, где $r$ — радиус вписанной окружности, $p$ - полупериметр.

1. Найдём площадь $\triangle ABC$:

$S_{ABC} = \frac{1}{2} \cdot AB \cdot AC \cdot sinA$, $S_{ABC} = \frac{1}{2} \cdot 10 \cdot 12 \cdot \frac{\sqrt{7}}{4} = 15\sqrt{7}$.

В $\triangle ABC$ по теореме косинусов $BC^{2} = AB^{2} + AC^{2} - 2AB \cdot AC \cdot cosA$.

По условию $\triangle ABC$ остроугольный, поэтому $cos A= \sqrt{1-(\frac{\sqrt{7}}{4})^{2}}=\frac{3}{4}$.

$BC^{2} = 10^{2} + 12^{2} - 2\cdot 10 \cdot 12 \cdot \frac{3}{4}$, $BC = 8$.

2. Найдём $p = \frac{P_{ABC}}{2} = \frac{10+12+8}{2} = 15$.

3. Расстояние между центрами окружности $OK = r = \frac{15\sqrt{7}}{15}$ $=\sqrt{7}$.

Ответ: $\sqrt{7}$.