На рисунке изображён график...

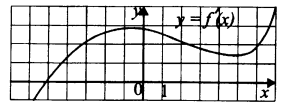
На рисунке изображён график $y=f'(x)$ - производной функции $f(x)$. Найдите абсциссу точки, в которой касательная к графику функции $y=f(x)$ параллельна оси абсцисс или совпадает с ней.

Пусть $x_{0}$ — абсцисса точки, в которой касательная к графику функции $y=f(x)$ параллельна оси абсцисс или совпадает с ней. Тогда значение производной $y=f'(x)$ в точке $x_{0}$ равно $0$, так как угловой коэффициент оси абсцисс $y=0$ равен $0$.

Но из графика видно, что $f'(x)= 0$ в единственной точке $x_{0}=-5$.

Действительно, прямая $y = 0$ пересекает график функции $y=f'(x)$ в единственной точке $(-5; 0)$, абсцисса которой равна -$5$.