ЕГЭ по Математике (профильный)
Найдите площадь поверхности прямой...
Задание:
Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными $4$ и $3$, и боковым ребром, равным $8$ (см. рис.).
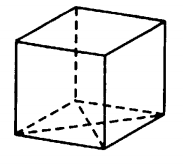
Решение:
Площадь боковой поверхности призмы находим по формуле $S_{бок.}= P_{осн.} \cdot h = $ $4a \cdot h$, где $P_{осн.}$ и $h$ — соответственно периметр основания и высота призмы, равная $8$, и $a$ — сторона ромба. Найдём сторону ромба, пользуясь тем, что диагонали ромба взаимно перпендикулярны и точкой пересечения делится пополам.
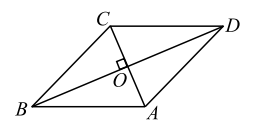
Из треугольника $BOC$ (см. рис.) по теореме Пифагора находим $BC^{2} = BO^{2} + OC^{2} =$ $(\frac{4}{2})^{2} + (\frac{3}{2})^{2} =$ $4+ 2,25 = 6,25$, $BC = 2,5$. Следовательно, $S_{бок.} = 4\cdot 2,5 \cdot 8 = 80$. $S_{осн.} = \frac{1}{2}\cdot AC \cdot BD =$ $\frac{1}{2} \cdot 4 \cdot 3 = 6$. Отсюда, $S_{пов. призмы} = 2S_{осн.} + S_{бок.} =$ $2 \cdot 6 + 80 = 92$.
Из треугольника $BOC$ (см. рис.) по теореме Пифагора находим $BC^{2} = BO^{2} + OC^{2} =$ $(\frac{4}{2})^{2} + (\frac{3}{2})^{2} =$ $4+ 2,25 = 6,25$, $BC = 2,5$. Следовательно, $S_{бок.} = 4\cdot 2,5 \cdot 8 = 80$. $S_{осн.} = \frac{1}{2}\cdot AC \cdot BD =$ $\frac{1}{2} \cdot 4 \cdot 3 = 6$. Отсюда, $S_{пов. призмы} = 2S_{осн.} + S_{бок.} =$ $2 \cdot 6 + 80 = 92$.
Ответ:
92
Задание добавил(а)
Создатель и главный администратор проекта ExamMe.
О задание:
Источник условия: Книга: Математика. Подготовка к ЕГЭ-2017. Профильный уровень. 40 тренировочных вариантов. Под редакцией Ф.Ф. Лысенко, С.Ю. Калабухова.
Источник решения: Книга: Решение заданий из книги указанной в источнике условия. Автор неизвестен.
Источник решения: Книга: Решение заданий из книги указанной в источнике условия. Автор неизвестен.
Обсуждения
Только зарегистрированные пользователи могут оставлять комментарии.
