Дана правильная четырёхугольная...

Дана правильная четырёхугольная пирамида $SMNPQ$ с вершиной в точке $S$, сторона основания равна $7$, а плоский угол при вершине пирамиды равен $90^{\circ}$.

а) Постройте сечение пирамиды плоскостью, проходящей через диагональ $NQ$ основания параллельно боковому ребру $PS$.

б) Найдите площадь сечения.

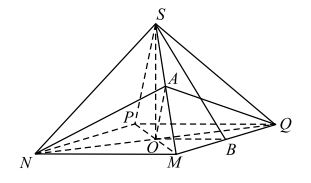
а) $PM$ пересекается с $NQ$ в точке $O$ (см. рис.), при этом $O$ — середина $PM$ и $NQ$. В плоскости $MSP$ проведём $AO\parallel SP$, она пересечёт $SM$ в середине ребра ($OA$ — средняя линия $\triangle PSM$). Точку $A$ соединим с точкой $N$, $AN$ лежит в плоскости $MSN$, точку $A$ соединим с точкой $Q$, $AQ$ лежит в плоскости $MSQ$. В плоскости $ANQ$ находится прямая $AO\parallel PS$, и по признаку параллельности прямой и плоскости получаем: $PS \parallel ANQ$. Плоскость $ANQ$ содержит диагональ $NQ$ и параллельна боковому ребру $PS$, то есть сечение $NAQ$ является искомым.

б) Докажем, что $\triangle ANQ$ — равнобедренный, то есть $AN = AQ$. Это следует из равенства треугольников $NAM$ и $AMQ$ (по двум сторонам: $MA$ — общая, $NM=MQ$ — и углу: $\angle NAM = \angle AMN$).

$NQ = 7\sqrt{2}$ как диагональ квадрата со стороной $NM = 7$. Проведём $SB \perp MQ$.

В $\triangle BSM: \angle SMB = 45^{\circ}$ ($\angle QSM = 90^{\circ}$; $\triangle QSM$ - равнобедренный), $\angle BSM = 45^{\circ}$, $SB=MN = \frac{7}{2}$. $MS = \frac{MB}{sin45^{\circ}} =$ $\frac{7}{\sqrt{2}}$. Точка $O$ — середина $NQ$, $AO \parallel SP$, $AO$ - средняя линия $\triangle MSP$, $AO = \frac{1}{2}SP$. $AO = \frac{7}{2\sqrt{2}} =$ $\frac{7\sqrt{2}}{4}$. $AO$ - высота $\triangle ANQ$, следовательно, $S_{сечения} = S_{\triangle ANQ} =$ $\frac{1}{2} NQ\cdot AO =$ $\frac{1}{2} \cdot 7\sqrt{2} \cdot \frac{7\sqrt{2}}{4} =$ $\frac{49\cdot 2}{8} = \frac{49}{4} = 12,25$.

Ответ: $12,25$.