При каких значениях параметра $a$...

При каких значениях параметра $a$ система

$\small \begin{cases} x-\sqrt{3}|y|=0, \\ (x-2a)^{2}+(y-cos\pi a)^{2} \leq (5a-21)^{2} \end{cases}$

имеет ровно два решения?

Решим задачу графически. Если $|5 — 2a| = 0$, то неравенство системы задаёт круг с центром в точке $(2a;cos\pi a)$ и радиусом $|5a-21|$. Если $|5a-21|=0$, то решением неравенства будет единственная точка: $x=2a = \frac{42}{5}$, $y=cos \pi a =$ $cos \frac{21\pi}{5}$, а тогда у системы не может быть более одного решения.

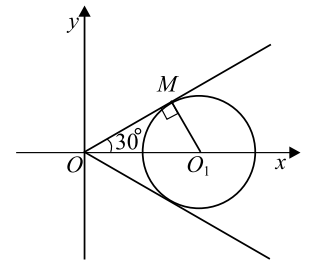
Уравнение системы задаёт угол (см. рис.), биссектрисой которого является ось $Ox$. Сторона этого угла проходит через точки $(0;0)$ и $(1;\frac{1}{\sqrt{3}})$ и поэтому образует угол $30^{\circ}$ с положительным направлением оси $Ox$.

Ровно два решения будет, если круг касается обеих сторон угла. Тогда центр круга должен лежать на биссектрисе угла, то есть на луче $Ox$. Следовательно, ордината центра круга должна равняться нулю, а абсцисса быть больше нуля. Ордината равна нулю, если $cos\pi a = 0$, $\pi a= \frac{\pi}{2}+\pi k$, $k \in Z$, $a = \frac{1}{2} + k$, $k \in Z$.

Абсцисса центра круга равна $2a$ и равна $2k+1$, она больше нуля, если $k\geq 0$. Рассмотрим $\triangle O_{1}OM$ где $O_{1}$ — центр круга. $M$ — одна из точек касания. Тогда $O_{1}M = |5a-21|$, $OO_{1}=2a$, $\angle O_{1}MO = 90 ^{\circ}$, $\angle MOO_{1} = 30^{\circ}$. Тогда $O_{1}M = O_{1}O\cdot sin\angle O_{1}OM=$ $2asin30^{\circ} = a$. Значит, $a = |5a-21|$, $k+ \frac{1}{2} = |5k + \frac{5}{2} - 21|$, $k+\frac{1}{2} =$ $|5k - \frac{37}{2}|$; отсюда либо $k+\frac{1}{2} = 5k - \frac{37}{2}$, то есть $4k = 19$, $k=\frac{19}{4}$; либо $k+\frac{1}{2} =$ $\frac{37}{2} - 5k$, $6k = 18$, $k = 3$. $k$ - целое число. $\frac{19}{4} \notin Z$; $3 \in Z$ и $3\geq 0$. Таким образом $k = 3$, $a= \frac{1}{2} + k = 3,5$.

Ответ: $3,5$